3

Conceitos Estatísticos

Estatística

Ao se deparar com um livro de estatística a primeira pergunta que muitos se colocam é o porquê de se estudar estatística. A compreensão da ciência estatística não se restringe apenas àqueles que precisam da estatística em sua prática profissional. O conhecimento da estatística é importante para a correta compreensão de comunicações de pesquisa, notícias e comunicações de dados. O conhecimento dos usos da estatística permite compreender a organização dos dados e a coerência no uso dos mesmos a cada caso(WITTE; WITTE, 2010). Dito de outra forma, a compreensão da estatística permite compreender descrições da realidade quando transcritas por meio de gráficos, tabelas de frequência e medidas de resumo.

Se todas as pessoas fossem iguais, se todos eventos seguissem sempre a mesma dinâmica, se todas transações possuíssem os mesmos valores; não haveria razão de ser da estatística. A estatística se dedica justamente a identificar toda variabilidade de ocorrências em cada população, seja uma população de pessoas, eventos, transações, etc. É possível afirmar que a estatística se ocupa de explicar questões como a variabilidade no QI, nas faixas de renda, nos índices de natalidade, mortalidade e nos eventos climáticos por exemplo.

O termo estatística pode ser utilizado tanto no sentido do senso comum que entende como estatística qualquer conjunto de dados; como no sentido científico e matemático, que entende a estatística como método de análise de dados (DOWNING; CLARK, 2002; MCCLAVE; SINCICH, 2013). Enquanto método científico a estatística pode ser definida pelas atividades de coleta, classificação, resumo, organização, análise, apresentação e interpretação de dados numéricos (BUSSAB; MORETTIN, 2017; MCCLAVE; SINCICH, 2013; RAMACHANDRAN; TSOKOS, 2009a).

Tais práticas consistem de ferramentas para obter informação em forma de dados organizados por meio de gráficos, tabelas, medias, intervalos, correlações, etc. para avaliar a informação, obter conclusões e orientar para a tomada de decisão (WITTE; WITTE, 2010). Algumas vezes o processo que vai da coleta à interpretação dos dados se utiliza da totalidade dos dados existentes, o que chamamos de dados populacionais; no entanto, na maioria dos casos, por questões de limites financeiros, operacionais e mesmo computacionais, este processo é realizado recorrendo a parcelas de dados obtidas a partir de uma determinada população, o que chamamos de dados amostrais, como veremos adiante.

Realidade e modelo

Antes de tratar da estatística propriamente dita, é preciso sempre ter consciência de que a análise estatística é sempre um modelo. Em qualquer análise o pressuposto básico para realizar um estudo é a diferenciação entre realidade e modelo.

Enquanto a realidade é um fenômeno complexo de difícil apreensão devido à sua dinâmica, complexidade e dimensão; um modelo é uma representação mais simples da realidade elaborado de acordo com um recorte específico que tenta dar conta de responder a uma determinada questão de pesquisa.

Considerando que a realidade é um fenômeno complexo, a resolução de problemas reais se torna uma tarefa difícil e por vezes impossível. Para tratar de fenômenos reais e complexos a ciência procura definir soluções aproximadas, no entando mesmo as soluções aproximadas são de difícil operacionalização dada a complexidade dos problemas reais; para contornar essa limitação os modelos são utilizados como cenários simplificados que permitem a obtenção de soluções exatas a partir de modelos propostos.

Dessa forma a realidade é simplificada por meio de modelos que permitam a obtenção de soluções exatas; sendo assim, um dos trabalhos da estatística, bem como da engenharia e outras ciências é buscar compreender o quanto uma solução exata de um modelo aproximado pode vir a ser uma solução aproximada de um problema exato.

Desse modo, a seleção, construção e avaliação de modelos é um processo determinante que permitirá a elaboração de bons modelos preditivos capazes de descrever questões e elaborar respostas (LEANDRO AUGUSTO SILVA; SARAJANE MARQUES PERES; CLODIS BOSCARIOLI, 2016).

Estatística descritiva e estatística infgerencial

Antes de se debruçar em cruzamentos, regressões, probabilidades condicionais e toda uma gama de operações sobre dados é preciso ainda definir a diferença entre estatística descritiva e estatística inferencial, e a decisão por estatística descritiva ou inferencial está ligado ao NÍVEL DE MEDIDA.

Pensando em nível de medida de certa forma ja estamos antecipando o tópico seguinte sobre tipos de variáveis. Basicamente existem dois níveis de medida, cda um possuindo seus subníveis e as técnicas apropriadas para cada nível.

Os níveis de pedida podem ser discriminados em nível qualitativo e nível quantitativo. O sível qualitativo opera a nível de categorias ou classes e pode ser entendido como a tarefa de classificar; já o nível quantitativo opera basicamente com fatos numéricos e pode ser definido como atividade de mensuração.

O nível de medida qualitativo opera sobre variáveis nominais e ordinais e utiliza técnicas chamadas de não paramétricas; enquqnato que o n’ ivel de medida quantitativo se ocupa de variáveis numéricas ordinais e intervalares por meio de técnicas paramétricas.

Uma vez estabelecidas as convebções sobre tipos de variáveis e níveis de medida, podem ser difinidas as aplicações da estatística descritiva e inferencial.

Estatística Descritiva

A estatística descritiva busca principalmente estabelecer a coleta, a organizazação, a exploração, o tratamento e a análise dos dados. De certaforma a estatística descritiva está muito ligada ao conceito de análise exploratória bem como ao processo de ETL (Extract, transform, load) ou extração, transformação, carregamento utilizado nas tarefas de machine learning e big data.

Estatística Inferencial

A estatística inferencial está muito ligada aos primeiros estudos que se ocuparam dos jogos de azar e a busca em prever os desfechos/resultados de uma série de jogadas. A estaística inferencial busca se utilizar de amostragens realizar análises e inferir/estrapolar para a população, ou seja a estatística inferencial não busca apenas descrever, mas generalizar os resultados de análises amostrais para o conjunto populacional.

Tipos de Variáveis

Tipos de Variáveis

Variáveis são características ou propriedades de uma unidade experimental ou observacional. Desse modo se pode considerar variáveis todas as características particulares presentes das unidades e que por serem particulares variam (MCCLAVE; SINCICH, [s.d.]). Cabe salientar que as variáveis possuem diferentes graus de volatilidade, algumas variáveis são bastante voláteis e podem apresentar uma grande amplitude de variação em curtos espaços de tempo, enquanto outras variam muito pouco,mas ao longo de grandes espaços de tempo; por exemplo a temperatura apresenta certa volatilidade, podendo variar significativamente ao longo de um único dia; enquanto que uma variável do tiposalário não varia com tanta frequência.

Existem muitos padrões de classificação de dados. Pode-se considerar um padrão de classificação de dados, a separação de dados em escala numérica e não numérica; outro padrão de dados muito utilizado é a classificação de dados de acordo com o período de sua obtenção ou realização. No primeiro caso os dados diferem por possuírem ou não escala numérica, no segundo caso os dados diferem por escala temporal. Para nossos propósitos iniciais utilizaremos a classificação das v.a. de acordo com sua escala numérica e não numérica. As v.a não numéricas ou categóricas são subdivididas em va. categóricas nominais e ordinais, v.a. categóricas são utilizadas para identificar categorias/propriedades enquanto que as v.a. ordinais são úteis para atributos de classificação/ranqueamento. As v.a. numéricas por sua vez se subdividem em v.a. numéricas discretas e contínuas, onde as primeiras são enumeráveis e as segundas são dados infinitesimais e, portanto, não enumeráveis

Tais peculiaridades nos tipos de v.a permitem elaborar análises sobre dados de um único período temporal, mas com distintas escalas numéricas e não numéricas, formatando o que se convenciona chamar de dados de corte transversal; bem como a conveniência na utilização de dados numéricos e não numéricos em diferentes períodos temporais, permitindo a realização se séries temporais (RAMACHANDRAN; TSOKOS, 2009b). Para nossos propósitos iniciais utilizaremos a classificação mais usual, que utiliza apenas a classificação das v.a. em numéricas e categóricas. Como as v.a. tanto numéricas como categóricas são subdivididas em duas subcategorias, tais características norteiam a decisão sob quais técnicas estatísticas devem ser tomadas para tratamento e resumo das mesmas (BUSSAB; MORETTIN, 2017), como veremos adiante.

Variáveis Categóricas

Variáveis Nominais

Descrevem atributos que qualificam as aunidades observacionais, sem que exista ordenação ou ranqueamento entre as unidades observadas.

Variáveis Ordinais

As variáveis ordinais representam características que ordenam ou ranqueiam os indivíduos, embora as mesmas não possam ser confundidas com números. São variáveis ordinais a ordem de classificação, o grau de instrução, etc.

Variáveis Quantitativas

Variáveis Intervalares (Contínuas)

São aquelas variáveis em que seus valores se encontram em intervalos de números reais, sendo resultado de alguma mensuração. A nível intervalar as categorias de mensuração possuem distâncias iguais, no entando a utilização de medidas intervalares não garante que um número seja o dobro do outro, assim 20º não é exatamente o dobro de 10º (não há um zero absoluto), essa proporcionalidade só acontece no nível de medida de razão.

Variáveis de Razão (Discretas)

São variáveis numéricas as quais formam um conjunto finito, como por exemplo a lista de alturas de uma turma de jogadores de basquete. Dito de outra forma as variáveis discreta representa um conjunto de variáveis enumeráveis com distâncias iguais e ainda com um zero absoluto. A nível intervalar, a medida de gráus célsius 0º não é um zero absoluto, me exigindo uma outra escala para zero absoluto (Kelvin).

Conjuntos

Variáveis Dependentes e Independentes

Variáveis independentes (preditivas) podem ser descritas como as variáveis que o pesquisador manipula, enquanto que variáveis dependentes são variáveis cujo resultado (desfecho) é mensurado em função da manipulação das variáveis independentes. Muitas vezes não há como manipular uma variável independente, nesse caso o processo adotado é observar estas variáveis como elas ocorrem naturalmente e como estas afetam a variável depedente. Por exemplo, uma análise pode ser realizada observando o quanto a variação no nível de renda das famílias influencia no grau de instrução dos membros das famílias.

População e amostra

População

População é todo conjunto de elementos que compartilham pelo menos uma característica. Quando nos referimos a população nos referimos ao conjunto total unidades informacionais que constituem um universo de pesquisa. Quando nos referimos à população os termos que descrevem suas medidas de média, moda, distribuições, etc., são chamados parâmetros. Quando possuímos os parâmetros de uma população e conhecemos a distribuição dos fenômenos a ela associados, podemos a estimar a probabilidade de ocorrência de um dado fenômeno seja a nível de indivíduo, seja em um grupo estratificado. O conceito de população pode ser definido como o conjunto de todos indivíduos ou elementos de um grupo de interesse, tais como todos elementos da população de uma cidade, estado ou país; também constituem uma população a totalidade de bens produzidos em um determinado período. Logo, população é o conceito que define o conjunto total de observações ou potenciais observações de um determinado escopo de análise. Outros exemplos de população podem ser: todos pratos contidos no menu de um restaurante, conjunto de eleitores, totalidade de alunos de uma instituição de ensino, total de acidentes em um ano, eventos climáticos em um dado período, operações de um dado ano na bolsa de valores. Pelo exposto, conclui-se que populações podem ser constituídas de pessoas, objetos, transações e eventos (MCCLAVE; SINCICH, [s.d.]). Quando um estudo consiste da análise de uma população, realiza-se o registro de todas unidades contidas na população e o registro de todos os atributos de interesse de cada unidade constituinte da população, o que se costuma chamar de censo. Quando uma dada população é muito extensa, ou a obtenção de todos os dados da mesma é muito caro ou trabalhoso recorre-se a utilização de subconjuntos da população denominados de amostra. Comumente costuma-se compreender população como um conjunto populacional adscrito, enquanto que para a ciência estatística uma população é uma abstração que se constitui de qualquer conjunto de propriedades e medidas de interesse quando considerada a totalidade das ocorrências das mesmas.

Amostra

O conceito amostra diz respeito a um subconjunto de indivíduos ou elementos constituintes de uma população e que foram retirados da mesma de forma prescrita (DEVORE, [s.d.]). Esse subgrupo ao ser extraído de uma população é obtido utilizando técnicas que permitam extrair conjuntos de dados de máxima verossimilhança com as características da população de origem. Esta exigência se faz necessária porque o papel da amostra é representar um conjunto de dados com o menor custo possível, mas que ao mesmo tempo permita obter inferências para toda a população, assim, busca-se por meio de amostras obter a variabilidade de características que satisfaçam a necessidade de descrever uma dada população. Existem muitos exemplos amostrais no nosso cotidiano. Quando lemos sobre uma pesquisa de intenção de votos em uma disputa eleitoral estamos diante de uma amostra. Essas amostras consistem em coletar as intenções de votos de algumas centenas de eleitores. Para que esta amostra apresente resultados satisfatórios este conjunto de eleitores entrevistados deve ser selecionado de modo a conter todas as características demográficas da população de interesse, dessa forma busca-se criar um grupo que seja uma representação de toda variabilidade na população de interesse e assim permitir obter a estimativa das intenções de voto daquela população de acordo com os perfis que a constituem. Este tipo de procedimento permite predizer possíveis resultados a partir das generalizações obtidas por meio da análise amostral, onde em última análise o que se faz é utilizar amostras para aprender sobre populações (MCCLAVE; SINCICH, 2013). Um exemplo de uma pesquisa amostral e de quais desdobramentos podem derivar da mesma é a pesquisa que demonstrou que 41% da audiência dos canais de TV aberta possui 50 anos ou mais e que a faixa etária ente 12 a 24 anos é a que representa a menor audiência dos canais abertos. Este exemplo demonstra uma pesquisa em que a população de interesse é a audiência de canais de TV aberta; onde a variável de interesse é a idade; em que a amostra é constituída de indivíduos selecionados da população que constitui a audiência de canais abertos e que por fim considera como descrição inferencial para generalização a faixa etária da audiência. Um desdobramento dessa pesquisa poderia ser uma amostragem da audiência de TV paga ou canais de estreaming, visando identificar o perfil de idade dessas audiências. Nesse novo cenário, a população seria a audiência de canais pagos ou de canais de streaming, a variável de interesse continuaria sendo a faixa etária da audiência, o conjunto amostral consistiria da retirada de indivíduos da população alvo e novamente a descrição inferencial dessa amostra seria conhecer a média de idade da audiência dessas populações. O exemplo acima é constituído de um processo de descrição e outro inferencial. A descrição amostral neste caso, consiste em descrever as respostas da amostragem da audiência. Para ambos exemplos o processo realizado envolve uma inferência de interesse, que consiste em generalizar para a população os resultados obtidos na amostragem.
Toda amostragem enquanto processo de coleta de dados e construção do conhecimento consiste de cinco elementos; são eles, uma população de interesse, uma ou mais perguntas a serem respondidas, uma amostragem da mesma população, inferências derivadas dos resultados da amostra e medidas de confiabilidade. Como o processo de amostragem consiste em obter informações generalizáveis para toda a população a partir de uma parcela da mesma, este processo requer o uso de medidas de confiabilidade; estas medidas são técnicas quantitativas que nos dão o grau de incerteza associado a uma dada inferência amostral (MCCLAVE; SINCICH, 2013). É interessante observar que um mesmo conjunto de informações pode ser considerado como população ou amostra a depender dos propósitos do estudo ou análise em questão. O número de veículos estacionado em um estacionamento privado pode ser considerado como uma população quando se trata de um conjunto de veículos tomado para estimar a capacidade de acomodação daquele espaço, no entanto estes mesmos veículos podem ser tomados como uma amostra quando se quer estimar a dimensão média dos veículos de proprietários que utilizam garagens privadas. Muitas populações são extremamente grandes e dessa forma apenas informações potenciais são possíveis de serem obtidas por meio de amostras. Estas informações potenciais constituem amostras que servem de base de informação para estimar os padrões distributivos da população a ser considerada.

Dica

Os parâmetros populacionais costumam ser simbolizados por letras gregas, enquanto que as estatísticas costumam ser identificadas por letras do alfabeto latino. Uma boa maneira de lembrar esta regra é que; poucos conhecem os parâmetros de uma população, assim como poucos conhecem o alfabeto grego, da mesma forma há maior facilidade em conhecer o alfabeto latino, como também é mais fácil obter os valores de uma amostra.

Estatística Descritiva e Inferencial

Como visto anteriormente, a estatística possui sua razão de ser na evidencia da variabilidade dos fatos, e para compreender esta variabilidade a estatística se utiliza de conjuntos amostrais e conjuntos populacionais e nesse sentido, a abordagem sobre estes conjuntos de dados difere à medida que manipulamos estes diferentes conjuntos. Por isso a estatística pode ser dividida em duas áreas: estatística descritiva e estatística inferencial. Tanto a estatística inferencial como a estatística descritiva partem de uma unidade mínima, a unidade experimental ou observacional. Como unidade experimental ou observacional entende-se uma unidade ou objeto tais como pessoa, coisa, transação ou evento. Uma população consiste da totalidade de unidades de um fenômeno de interesse e uma amostra de uma parcela da população; ou seja, enquanto a população reúne o conjunto das unidades experimentais ou observacionais, a amostra reúne apenas uma parcela das mesmas.

Estatística Descritiva

Podemos dizer que quando tomamos uma população sob análise, os dados refletem integralmente a variabilidade da mesma população. Para descrever esta variabilidade, utilizam-se gráficos e tabelas e medidas de resumo para descrever padrões e resumir dados. Estas atividades constituem o campo da estatística descritiva. A Estatística descritiva é uma maneira conveniente de apresentar informações. Órgãos de imprensa, informativos e outros meios de comunicação recorrem à estatística descritiva para apresentação de dados de forma sucinta. Outro uso da estatística descritiva é fornecer subsídios para cálculos probabilísticos, uma vez que, as conclusões obtidas a partir desses dados, permitem descrever os padrões e a variabilidade do conjunto populacional; o que por sua vez, permite estimar a probabilidade de que um elemento qualquer retirado aleatoriamente da mesma população, possa conter determinadas características contidas no espaço de possibilidades existentes na população.

Estatística Inferencial

Quando lidamos com conjuntos amostrais, abrimos mão da reter todos dados existentes em relação ao objeto de estudo, e recorremos a ferramentas que permitam por meio de amostragens, reproduzir a variabilidade da população. Este salto é obtido por meio de métodos de estimação, predições e generalizações capazes de dar subsídios para a tomada de decisão (MCCLAVE; SINCICH, [s.d.]). A área mais avançada da estatística é aquela relacionada à realização de inferências (WITTE; WITTE, 2010), justamente porque as ferramentas inferenciais permitem que se faca a partir de conjuntos de dados relativamente pequenos, observações capazes de descrever características de populações inteiras. A diferença entre as abordagens populacionais e amostrais consiste em, partir dos dados populacionais para obter probabilidades individuais ou distributivas; enquanto que por meio de conjuntos amostrais busca-se inferir dados populacionais por meio de elementos de probabilidade que garantam com um certo grau de certeza que a informação obtida através da realização amostral seja representativa do todo (Figura 1).

População x Amostra

Muitas questões são levantadas sobre o porquê de recorrer a amostragem e não ao estudo populacional. Muitas vezes as populações são muito extensas e o processo de coleta e análise se torna dispendioso. Outro fator determinante para se recorrer a amostras esta relacionado ao fato de que o processo de análise pode destruir todo conjunto populacional, por exemplo: se realizarmos um teste de resistência de materiais é possível que todos elementos do estudo sejam inutilizados. Se realizarmos uma análise de resistência de vigas, podemos acabar por destruir todo o conjunto populacional. Outro fator que favorece a decisão por utilizar dados amostrais é a possibilidade de obter maior precisão em testes amostrais, dado que é possível obter maior controle sobre o experimento (DOWNING; CLARK, 2002).

Embora a estatísticas descritivas sejam muitas vezes associadas a dados de populações, a estatística descritiva também é utilizada em amostragens quando de deseja descrever e resumir os dados amostrais por meio de tabelas, gráficos e medidas de resumo. Da mesma forma há a tendência de associar técnicas inferenciais às análises amostrais, mas nem sempre é assim. Quando tomamos uma dada população como domínio de estudo em diferentes períodos, construímos o que se costuma denominar uma série temporal, onde descrevemos os padrões e distribuições da mesma população a cada período como minutos, horas, dias, meses, anos ou décadas; a depender de que tipo de população estamos a tratar. Este tipo de análise consiste em comparar o quanto estes padrões de uma população variam ao longo das unidades de tempo definidas, visando identificar a amplitude dessas variações. As comparações por meio de séries temporais constituem técnicas inferenciais, quando as mesmas comparações buscam inferir padrões de variação da distribuição da população ao longo do tempo. Por exemplo, quando consideramos o censo demográfico brasileiro; a população de idosos com 65 anos ou mais em 1991 era de 4,8%, passando em 2000 para 5,9% e chegando em 2010 a 7,4%. Estes dados quando estimados dentro de um determino intervalo de confiança permitem inferir que a população brasileira passa por um processo de envelhecimento. Tal abordagem parte de três estatísticas descritivas de uma população que quando acompanhada de técnicas adequadas de análise e estimação geram inferências que permitem afirmar que tal variação não é fruto de acaso no computo das frequências de indivíduos contidos em cada faixa etária, mas que se tratam de fato, de um fenômeno de alteração do perfil demográfico da população brasileira.

Eventos Aleatórios

É a porção de todos os eventos pertencentes a um espaço amostral, ou seja, todos aqueles resultados possíveis em um dado experimento. Ao lançarmos uma moeda o espaço amostral é unicamente cara ou coroa S={K, C}. Assim como ao lançarmos um dado o espaço amostral é dado por S={1,2,3,4,5,6}.

Conjuntos

Os conjuntos nada mais são do que classes de dados. Quando tratamos de fenômenos matemáticos sempre tratamos de dador oriundos de fenômenos aleatórios ou determinísticos (MORETTIN, 2010). Como determinísticos entendemos fenômenos que sempre apresentam os mesmos resultados e aleatórios aqueles eventos em que o resultado não é conhecido, ainda que compreendidos dentro de um espaço de probabilidades. Em estatística e probabilidade antes de qualquer análise, interessa saber qual o espaço amostral do fenômeno tomado sob análise. O espaço amostral consiste no conjunto de eventos ou desfechos possíveis de um experimento. Cada desfecho se constitui de um ponto amostral e a reunião de diversos pontos amostrais constitui um conjunto que pode conter como resultados a reunião de todos eventos possíveis um uma porção deles.

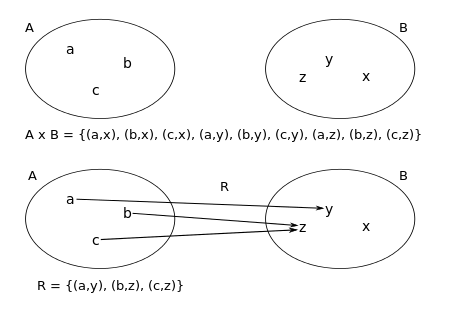
Conjuntos

n(AuBuC) = n(A)+n(B)+ n(C)-n(AnB)-n(Anc)-n(BnC)+n(AnBnC) Aqui quando realizamos A união com B estamos adicionando duas vezes os valores comuns a ambos os conjuntos, assim, subtraímos uma vez a intersecção de A e B de forma a eliminarmos a sobreposição de valores em (A u B). Esta definição nos leva ao seguinte teorema: (AuB)=n(A)+ n(B)-n(AnB) Isso significa que somamos a área de A e B, mas subtraímos as N vezes que se sobrepõem menos 1. Assim (AuB)=n(A)+ n(B)-n(AnB) onde, N = E((AnB))-1. Dessa forma se tomarmos três conjuntos de dados A, B e C; teremos a área de (A + B + C – N). Onde haverá uma região de intersecção de A+B+C então N= 3-1, significando que os dados comuns ao grupo A, B e C foram acionados três vezes, restando eliminar duas sobreposições e manter apenas uma ocorrência dos eventos em comum; nesse caso estamos falando de “A n B n C”. Cabe salientar que além da intersecção de A+B+C, nesse exemplo temos a intersecção de A+B-C, A+C-B e ainda B+C-A, como demonstrado na Figura 3. Note que se considerarmos as áreas dos conjuntos A, B e C a soma dos três conjuntos é significativamente superior à área que a disposição dos mesmos realiza de fato. Ao adicionarmos A+B, A+C e B+C duas vezes esta duplicidade precisa ser corrigida por meio da subtração apropriada e esta subtração será n-1 vezes a ocorrência dessa sobreposição. Significa dizer em termos práticos que: (A u B u C) = A + B + C – ((A n B)+(A n C)+(C n B)+2*(A n B n C)):

Como apresentar dados

No mundo contemporâneo o volume e a variabilidade de dados armazenados crescem de forma exponencial, superando a capacidade de assimilação humana. Dessa forma muitas técnicas de coleta e análise de dados visam justamente tornar esta quantidade de informação em meios mais adequados para a assimilação e interpretação humana. Todo e qualquer dado somente é útil quando servir para aprender sobre algo ou para a tomada de decisão a respeito de alguma questão, de outra forma toda informação se torna inútil. Assim, toda coleta de dados se presta a resumir dados, testar hipóteses e apresentar conclusões (GLANTZ, 2012). A apresentação de dados para atender aos propósitos humanos consiste de três pilares: a apresentação deve ser realizada de forma clara, concisa e acurada (BARROW, 2006). Para realizar uma boa análise de dados, duas etapas são bem demarcadas e fundamentais. A primeira etapa da análise de dados consiste em resumir os dados e obter as primeiras representações da distribuição das características que constituem nosso domínio de interesse. O segundo momento da análise de dados busca medidas de centralidade, de dispersão e correlação, ou seja, valores médios, de variabilidade no cenário considerado e as prováveis associações entre os diferentes atributos que compõem o domínio.

Distribuições de Frequência Relativa (f.r.)

Quando computamos o número total de registros de uma v.a. qualquer, estamos enumerando as ocorrências da v.a. de interesse. Uma distribuição de frequência nada mais é do que a enumeração de observações realizadas, porém, quando as distribuímos de acordo com suas classes de pertencimento, obtemos a distribuição de frequências por classe ou o número de observações contidas em cada classe, o que se convenciona chamar de frequências relativas. O uso de distribuições de frequência é bastante comum; por exemplo, a contagem de uma turma de 45 alunos apresenta a frequência absoluta geral de 45, que nada mais é do que a enumeração de todos os alunos. Ao distribuirmos os alunos de acordo com a classe sexo, poderíamos ter a frequência de alunos do sexo masculino e feminino semelhante a M=21 e F=24, onde as proporções dessa distribuição correspondem a 0.466 e 0.533; representando respectivamente as frequências relativas por sexo, obtidas pelo cálculo simples de (21/45) e (24/45) conforme a Tabela 1: Frequências Absoluta e Relativas da Variável Aleatória Sexo. Da mesma forma poderíamos obter para a mesma turma a distribuição relativa de reprovados em nenhuma, uma, duas ou três disciplinas, que poderiam resultar na seguinte distribuição de frequências S={nenhuma = 26, uma=10, duas=6, três=2} e na distribuição relativa proporcional de frequências S={nenhuma = 0.577, uma=0.222, duas=0.133, três=.044} conforme a Tabela 2: Frequências Absoluta e Relativas da Variável Aleatória Reprovação. Para o exemplo utilizado obteve-se as frequências absoluta e relativa de acordo com cada classe observada. O uso de frequências relativas pode ser obtido tanto pelo cálculo de proporções como exemplificado acima, como também por meio de percentuais em que os mesmos cálculos são obtidos apenas multiplicando as proporções iniciais por 100, movendo o ponto decimal duas casas para a direita. Quando utilizamos percentuais a escala de valores relativos varia entre 0 e 100; enquanto que quando utilizamos proporções, os valores relativos variam ente 0 e 1. No exemplo utilizado, basta realizar os seguintes cálculos (0.466100) = 46.6% e (0.533100) = 53.3%. Assim a soma de todas as proporções das classes de uma v.a. resulta em 1 e a soma de todos percentuais resulta em 100, lembrando que o uso de proporções ou percentuais é uma decisão do pesquisador visando uma melhor representação e interpretação dos dados.

….

…

O uso de frequências relativas é muito útil quando há o interesse em comparar duas populações ou amostras de tamanhos distintos, pois as frequências relativas permitem utilizar para ambos os conjuntos a ser comparados a mesma escala de 0% a 100% ou de 0 a 1; em que cada classe será sempre constituída de um percentual ou fração da frequência total. ## Frequências Cumulativas Da mesma forma que se utilizam as frequências relativas, a depender da necessidade, podem ser utilizadas frequências cumulativas (f.c.). Frequências cumulativas consistem no somatório das classes consecutivamente até atingir o total como visto na Tabela 3: Frequências Cumulativas. Como pôde ser visto, na tabela as distribuições de frequência cumulativas apresentam a frequência de ocorrências de cada classe acrescidas à soma de todas as frequências precedentes.

…

Quando trabalhamos com distribuições cumulativas de dados categóricos ordinais, é importante ordenar a tabela de acordo com a ordem hierárquica da tabela de modo a compreender a distribuição cumulativa de acordo com a ordem das classes. Como exemplo de distribuição cumulativa de uma v.a. categórica ordinal, podemos tomar o exemplo de uma empresa constituída de estagiários, assistentes, engenheiros, gerentes, diretores e presidente. Para este cenário poderíamos ter uma distribuição como na Tabela 4: Frequências Cumulativas de Variáveis Aleatórias Categóricas Ordinais. A disposição de tabelas de v.a. ordinais como exemplificado permite extrair informações tais como, qual o número de colaboradores abaixo da categoria gerencial, a resposta nesse caso é imediata, representando 92 colaboradores, uma proporção de 0.91 e o percentual e 91.09%. Também é possível concluir pela tabela que os cargos de nível de gestão correspondem a 1-0.9108; uma proporção de 0.0891 ou 8.91%.

…

Quando os dados são atribuídos a classes de valores singulares como nos exemplos acima, obtemos distribuições de frequência de dados desagrupados (WITTE; WITTE, 2010). Lembrando que o uso de dados desagrupados é útil quando o número de classes de uma v.a. é pequeno. Usualmente utilizam-se dados desagrupados para conjuntos de até 20 classes (WITTE; WITTE, 2010).

Dados Intervalares

Para v.a. com mais de vinte classes, recomenda-se o uso de frequências de dados agrupados. Esta técnica consiste em criar intervalos de dados, e, portanto, constitui-se como uma técnica para v.a. numéricas que permitam criar estes intervalos, em que todos os valores contidos no intervalo são considerados pertencentes a uma mesma classe. Uma distribuição de frequências de pressão arterial (P.A.) é um bom exemplo de uso de frequências de dados agrupados. Como a mensuração de P.A. é obtida em mm de mercúrio, podemos obter dados como S={105,114,116,123, 126, 128, 130,131,134,136,142,145}. Como a P.A. é um tipo de v.a. com amplo espaço amostral que pode assumir algumas dezenas de valores possíveis; convém criar classes com intervalos tais como [100 – 110), [110 – 120), [120 – 130), [130 – 140), [140 – 150), com intervalos de 10 possíveis valores, em que o primeiro valor representado está contido no intervalo e o segundo não – o que se denomina limite superior aberto. Neste novo arranjo a frequência de valores passa a ser constituída pela soma de todas as frequências de valores contidos no intervalo. Este tipo de abordagem facilita a identificação de picos, demonstrando os intervalos de maior ocorrência das v.a. consideradas.

A representação de intervalos pode ser feita de duas maneiras como no caso [110 – 120), em que pode ser lido o intervalo de 110 a 120, excluindo-se 120; ou como no segundo caso [110-119], que pode ser lido como o intervalo de 110 a 119. Em qualquer uma das opções, cada mensuração é atribuída a uma e somente uma classe intervalar definida. Deve ser observado que os intervalos devem sempre seguir a mesma escala de medida da v.a. em questão. Em alguns casos os limites inferior e superior podem ter seus valores mínimo e máximo respectivamente omitidos em função da possibilidade de ocorrência de valores extremos que serão atribuídos aos limites intervalares extremos. Ao se utilizar dados intervalares é necessário compreender que entre um intervalo e outro, localiza-se o limite real, que fica localizado no ponto médio entre os limites de dois intervalos. No exemplo acima de P.A. o intervalo real entre 119 e 120 será a média desses dois valores limites, portanto (119+120)/2 = 239/2 = 119.5 (WITTE; WITTE, 2010). A definição do número de classes agrupadas é sempre uma questão crítica. Se criarmos intervalos com uma amplitude muito grande como [110-130), [130-116); corre-se o risco de mascarar a variabilidade contida nesse intervalo. E de outra forma, intervalos muito estreitos geram uma granularidade que pode gerar as mesmas dificuldades enfrentadas quando se utilizam dados desagrupados. Existem muitas técnicas para criar intervalos, como separá-los por dezenas, centenas, ou mesmo calcular a amplitude da variável (subtrair o menor valor do maior valor) e após obter a raiz quadrada da mesma. Como no caso de P.A. se o menor valor registrado fosse 104 e o maior 198 o cálculo de intervalos pode ser obtido calculando a raiz de 198-104, ou seja, a raiz de 94 = 9,69, arredondando-se o valor obteríamos 10 classes. Segundo (WITTE; WITTE, 2010) um outro modelo é definir um número de classes a ser trabalhado e obter o quociente da amplitude da v.a pelo número de classes definidas. Por exemplo no exemplo acima em que se obteve o intervalo de 94 e se queira trabalhar com oito classes realizaríamos a divisão de 94/8, resultando em um intervalo de 11.75 a ser arredondado para o intervalo mais conveniente, que neste caso poderia ser 12 e então teríamos novos intervalos assim definidos [100 – 121], [122 – 133], [134– 145], [146 – 157], [158 – 169], , [158 – 169] , [170 – 181] , [182 – 193] , [194 – 205]. Quantos veículos trafegam em determinada via por dia, o número de voos por semana, o número de ocorrências policiais por mês, o número de nascimentos por estado; todos estes são exemplos de distribuições de frequência. As distribuições de frequência são úteis e um dos principais meios de identificação de padrões – quando estes existem. Distribuições de frequência podem ser apresentadas tanto por meio de gráficos como de tabelas, e a depender do tipo de dado um ou outro modelo de apresentação é mais adequado, como será visto adiante.

Outliers

require(ggplot2)

## Loading required package: ggplot2

aaa = faithful
names(aaa) = c("Veiculos", "Velocidade")
aaa$Velocidade[1] = 120
boxplot(aaa$Velocidade,main="Boxplot de Velocidades", 
        xlab="Velocidades Verificadas",horizontal = TRUE, col = "#0196A7")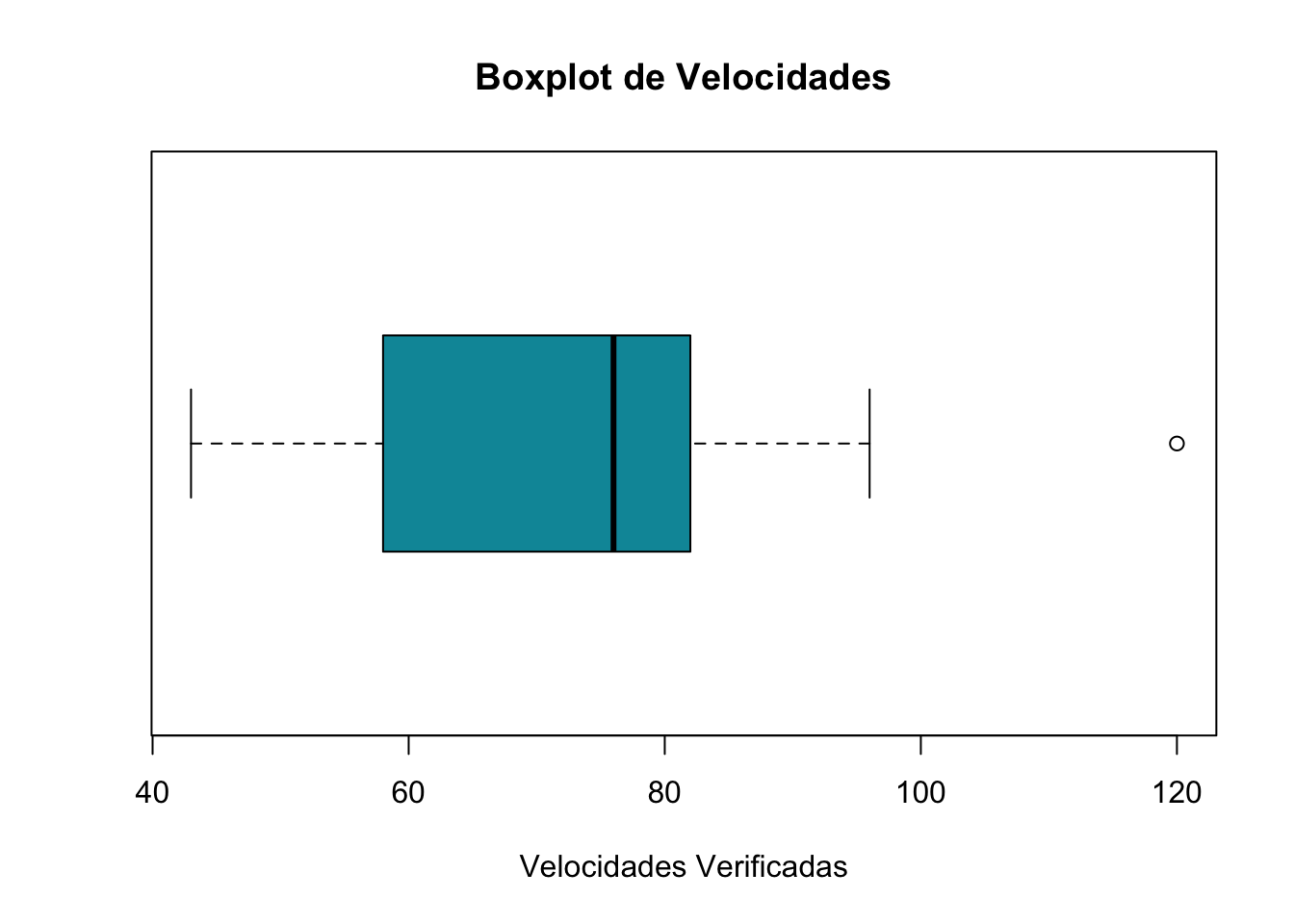

…

Muitas vezes no cotidiano ouvimos uma expressão que diz que algo “é um ponto fora da curva”, indicando que se trata de algo incomum. Os outliers são dados extremos, que são como os tais pontos fora da curva; eles representam dados atípicos, muito diferentes dos valores típicos da v.a. em questão. O exemplo da Figura 3: Gráfico de Barras demonstra um caso de outlier para o valor 120. Nesse caso o valor 120 destoa a distribuição amostral de modo a estar distante dos demais valores da v.a., este comportamento pode ser resultado de um evento raro, ou de um erro de registro ou mensuração do valor. A identificação de outliers é sempre recomendável para garantir a acurácia da análise da v.a., pois caso se verifique que o outlier se trata de erro de mensuração ou registro o mesmo deve ser eliminado da amostra ou corrigido caso seja possível auditar o dado. Uma outra possibilidade é, quando se tratar de um valor atípico, segregar este dado e apontar isso nas observações da pesquisa, garantindo que esta abordagem foi adotada de forma prescrita (WITTE; WITTE, 2010). É importante entender que muitas vezes um outlier pode ser um indicativo de um elemento a ser observado com maior atenção. A título de exemplo, uma pesquisa onde cada unidade observacional da v.a. de interesse seja o número de acidentes anuais em cruzamentos com ocorrências de tais eventos; caso a amostra apresentar valores típicos entre 3 e 9 e um determinado cruzamento apresentar um valor igual a 23, fica evidente que estamos diante de um outlier e que por se tratar de um outlier poderia ser eliminado ou isolado. Porém nem sempre deve ser assim; no caso exemplificado este dado deve ser objeto de atenção especial, justamente por se tratar de um ponto crítico que deve ser tomado em análise separadamente visando entender quais circunstancias tornam esta unidade observacional um valor atípico e por consequência um cruzamento de alto risco.

Dados Gráficos

Toda apresentação de dados busca responder uma questão, seja para atender uma análise exploratória, seja para identificar padrões e distribuições. Existe uma variedade de maneiras de organizar e arranjar dados, e na maioria dos casos elegemos aqueles com melhores padrões de visão e imediata compreensão. O meio de apresentação de dados por meio de gráficos visa permitir uma apresentação concisa e clara da informação a ser divulgada. Por meio de gráficos o reconhecimento de padrões se torna mais intuitivo ao mesmo tempo em que o volume e a magnitude dos dados são superados pela apresentação relativa da frequência dos dados. Dados contidos em grafitos podem ser facilmente identificados e as relações entre as diferentes categorias de dados podem ser identificadas mesmo por quem possui pouco conhecimento estatístico. Por meio de gráficos, podemos até mesmo mostrar representações mais claras de variáveis categóricas através da frequência da ocorrência das mesmas, fazendo com que variáveis não numéricas possam ser representadas em escala numérica de ocorrências/frequências.

Gráficos de barras

Gráficos de barras são uteis para representar dados numéricos e categóricos. Uma vez que dados categóricos se referem a classes as quais as unidades de análise pertencem e, portanto, não possuem uma escala numérica natural, os gráficos de barra permitem mensurar tais categorias em termos de frequência e percentuais como na Figura 3: Gráfico de Barras.

  ggplot(aaa, aes(x = Velocidade)) + geom_dotplot(aes(color = "#0196A7", fill = Veiculos), binwidth = 1.5) + ylab("Contagem") +  
  xlab("Velocidades Registradas")+  ggtitle("Velocidades de Veículos em Radar") + 
  theme_bw()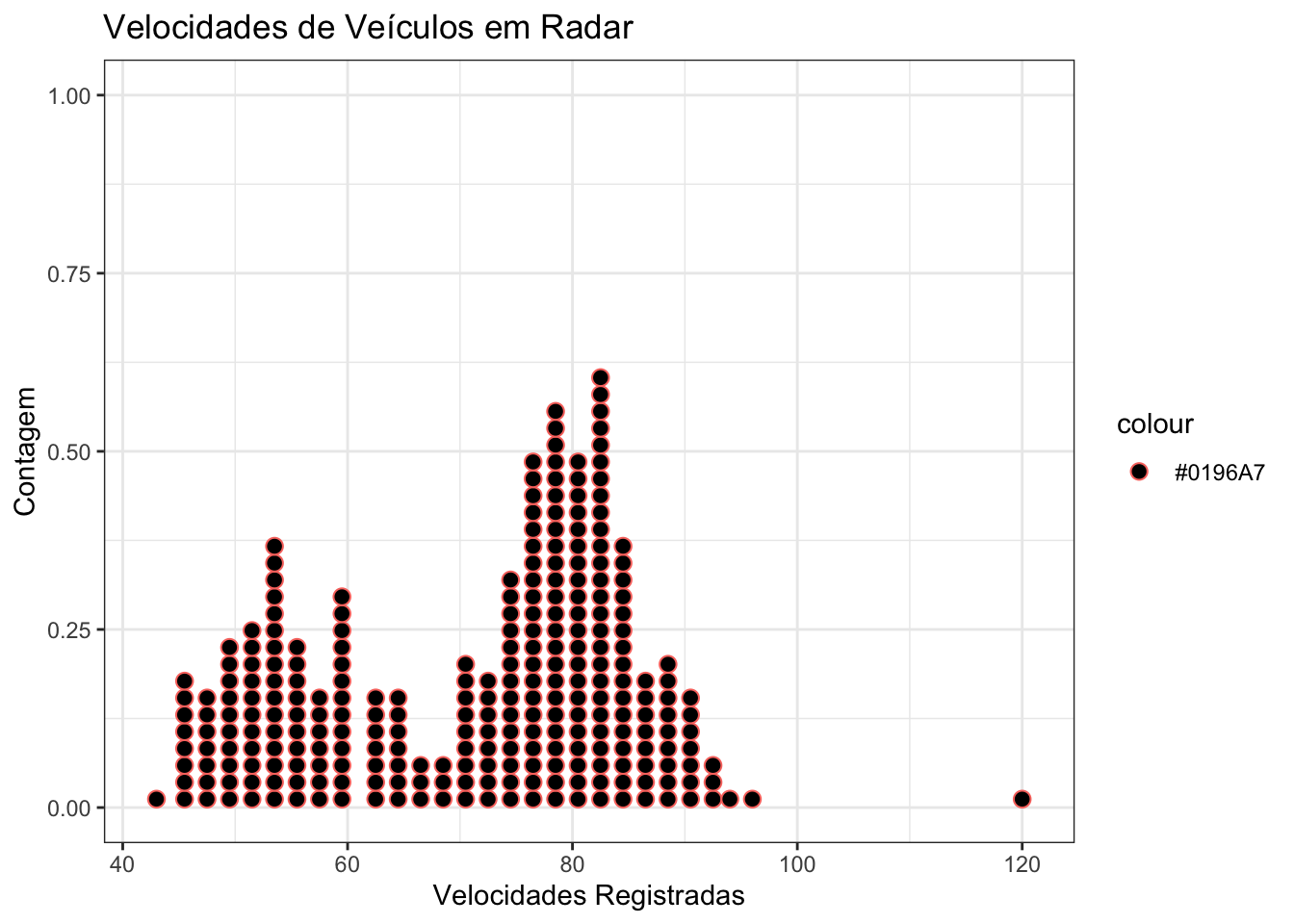 

Figura 3: Gráfico de Barras

Muitas pesquisas apontam que veículos equipados com air bags reduzem o número de fatalidades, mas reduzem quanto? Quando a resposta para esta questão precisa ser clara, breve e intuitiva o uso de gráficos se apresenta como uma ferramenta ideal. Os dados do artigo intitulado “Do Seat Belts and Air Bags Reduce Mortality and Injury Severity After Car Accidents?” de 2011 publicado no periódico “The American Journal of Orthopedics” aponta que em acidentes ocorridos nos EUA quando as ocupantes de veículos envolvidos em acidentes utilizam cinto de segurança e possuem dispositivo de air bag; a combinação dessas duas variáveis resulta em um redução de 67% das mortalidades, para aqueles que utilizam apenas o cinto de segurança a mortalidade em tais acidentes reduz em 50% e para aqueles ocupantes de veículos com air bag, mas que não utilizam cinto de segurança, a redução de fatalidades é de apenas 32%. A descrição estatística acima parece um pouco extensa e pouco clara, porém as mesmas informações contidas no gráfico da Figura 4: são mais intuitivos e proporcionam uma compreensão das relações de forma breve e esquemática demonstrando que a associação de air bag e cinto de segurança gera um fator protetivo nos ocupantes de veículos envolvidos em acidentes.

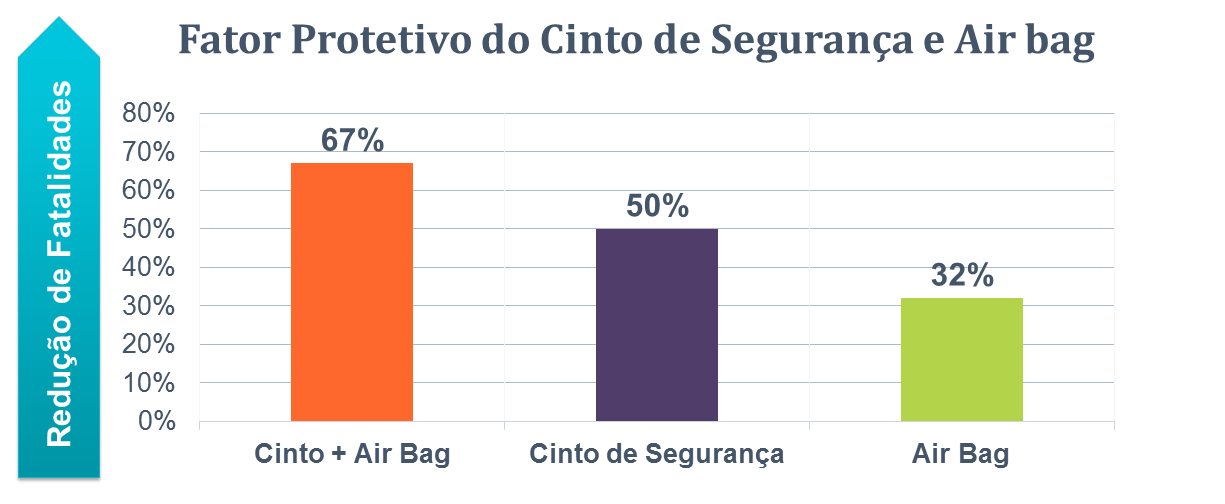
Figura 3: Figura 4: Redução da mortalidade em função de dispositivos de segurança

Gráficos de ramo e folhas

Quando utilizamos gráficos de barras, muitas vezes precisamos definir grupos e classes de forma arbitrária e a noção de quais são os valores reais da amostra a cada grupo as vezes fica imprecisa. Uma alternativa para superar esta dificuldade é o gráfico de ramo e folhas. Este tipo de gráfico permite verificar todos valores individuais de uma v.a. e ainda permitem ter uma visualização da forma de distribuição dos dados. Os gráficos de ramo e folhas são utilizados para dados quantitativos desde que estes possuam pelo menos dois dígitos. Esta técnica permite gerar uma representação visual de uma única variável de forma bidimensional, onde é possível identificar o formato real da distribuição de dados. Com os primeiros dígitos formam-se os ramos do gráfico e com os demais dígitos as folhas. Para isso os dados do ramo são relacionados em ordem decrescente na vertical e a cada valor correspondente na vertical são associados no seu eixo horizontal os seus valores complementares. Em uma escala de 10 a 200 os valores como 43 e 93 poderiam ser definidos de modo que os dígitos 4 e 9 pertençam pertencer à posição do ramo e ao seu lado como complemento estariam associados os valores 3 e 3. Dessa forma teríamos o ramo das dezenas e centenas e as folhas das unidades. Este modelo de gráfico possui como vantagens a possibilidade de identificar visualmente as possíveis assimetrias na distribuição dos dados bem como a garantia de que não se perde informação dos dados como acontece no caso de histogramas. Embora gráficos de histograma nos permitam conhecer a ocorrência de valores num dado intervalo, eles não permitem conhecer as verdadeiras pontuações individuais, enquanto que gráficos de ramos em folha permitem tanto conhecer a forma de distribuição das variáveis como conhecer os valores de cada ocorrência individualmente como se vê na Figura 5: Gráfico de Ramo e Folhas.

  stem(aaa$Velocidade) 

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##    4 | 3
##    4 | 55566666777788899999
##    5 | 00000111111222223333333444444444
##    5 | 555555666677788889999999
##    6 | 00000022223334444
##    6 | 555667899
##    7 | 00001111123333333444444
##    7 | 55555555666666666777777777777888888888888888999999999
##    8 | 000000001111111111111222222222222333333333333334444444444
##    8 | 55555566666677888888999
##    9 | 00000012334
##    9 | 6
##   10 | 
##   10 | 
##   11 | 
##   11 | 
##   12 | 0

Uma outra forma de apresentação do gráfico de ramo e folhas como apresentado na Figura 6: Gráfico de Ramo e Folhas Simplificado, onde se aplica uma simplificação após um número arbitrário de casos. Nesse caso, após a representação de oito unidades acrescenta-se um sinal de + acompanhado da contagem de números casos que complementam a linha.

  stem(aaa$Velocidade, width = 20) 

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##    4 | 3
##    4 | 55566666
##    5 | 00000111+12
##    5 | 55555566+4
##    6 | 00000022
##    6 | 55566789
##    7 | 00001111+3
##    7 | 55555555+33
##    8 | 00000000+37
##    8 | 55555566+3
##    9 | 00000012
##    9 | 6
##   10 | 
##   10 | 
##   11 | 
##   11 | 
##   12 | 0

Gráfico de setores

O gráfico de setores, também conhecido como gráfico de composição ou de pizza, é um excelente aliado para exibir percentuais de variáveis categóricas. Este tipo de gráfico consiste em um círculo dividido em setores onde cada um dos setores corresponde a uma das classes da v.a. em questão e cada setor do gráfico ocupa a área correspondente ao percentual ou proporção realizada por cada valor da v.a. categórica.  Esta forma de representação gráfica permite apreender como cada v.a. está distribuída em relação as diferentes categorias. Um exemplo de preferência por disciplinas em uma turma escolar poderia ser exibida como na Figura 7: Gráfico de Setores.

A relação matemática de um gráfico de setores com os dados representados é o ângulo de cada classe representada no gráfico. Este ângulo é obtido dividindo a frequência de cada classe pela frequência total de todas as classes e após multiplicando por 360: Ângulo = (frequência / frequência total) * 360.

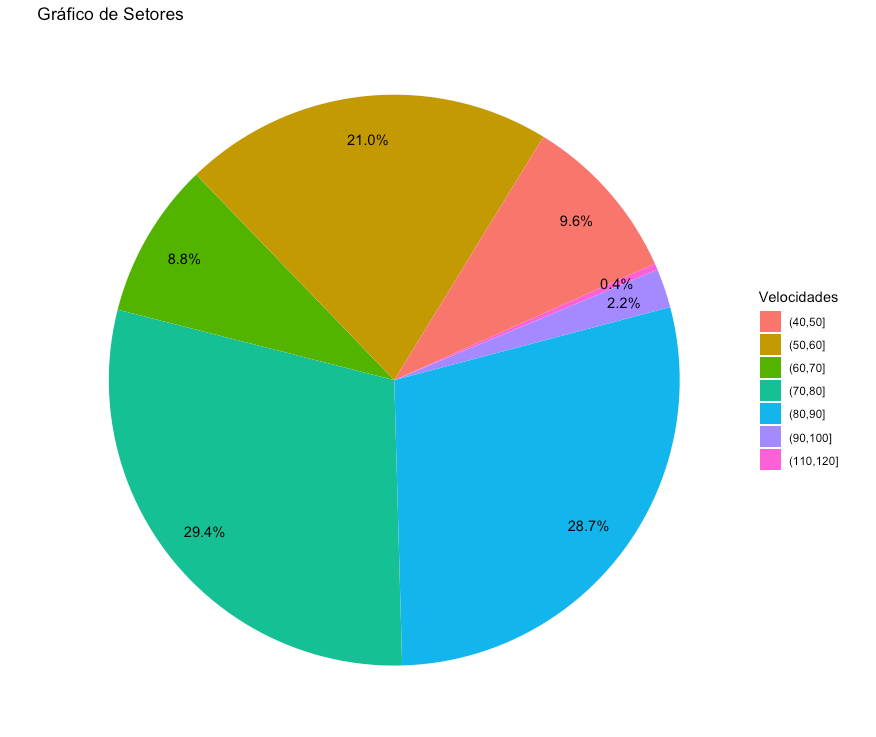
Figura 7: Gráfico de Setores

pie.data = c(12,16,25,11,6,4)
pie(pie.data)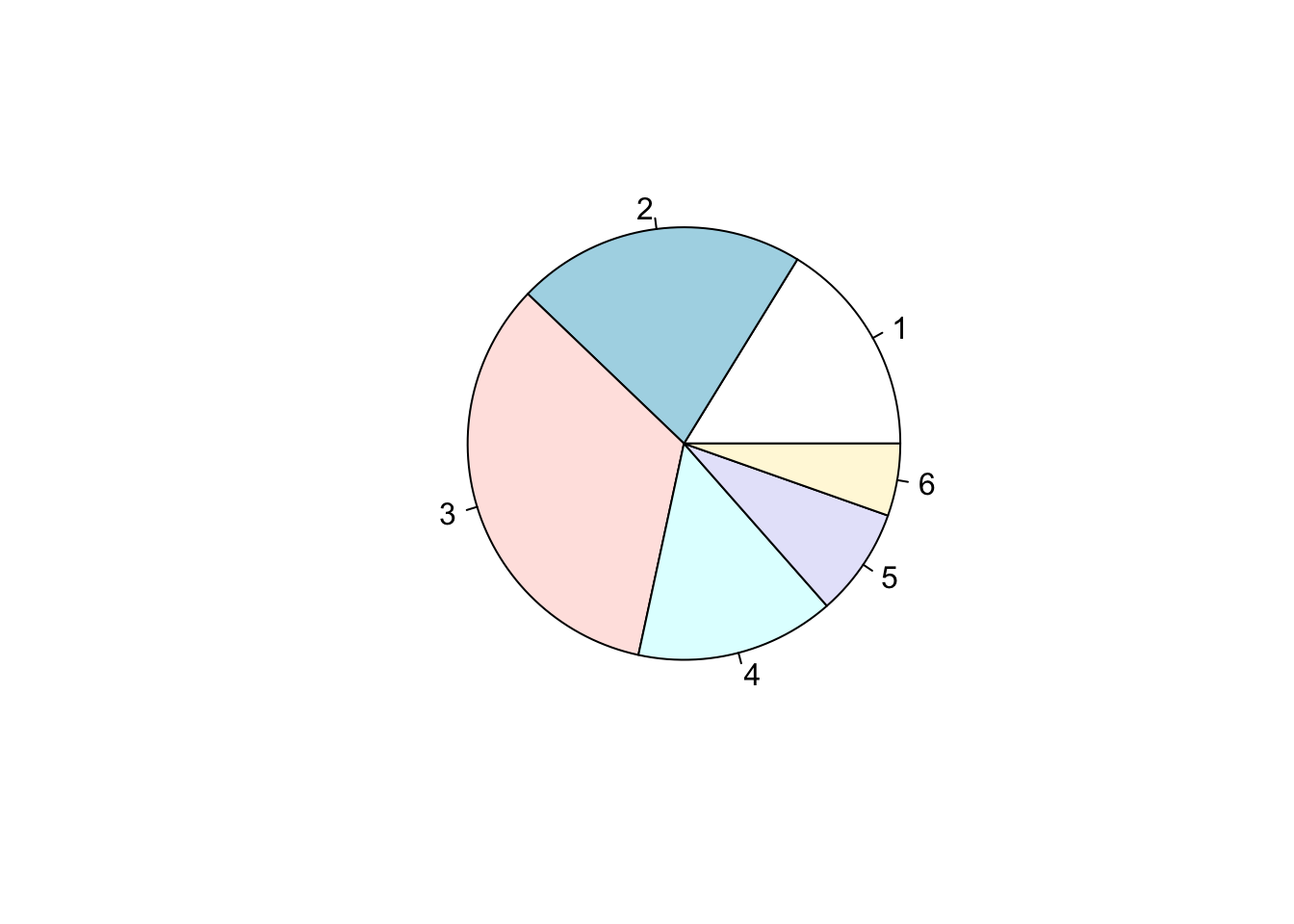

pie(pie.data, clockwise=TRUE, col= c("red", "orange", "yellow", "green", "blue", "purple"))
title(main="Gráfico de Setores", font.main= 4)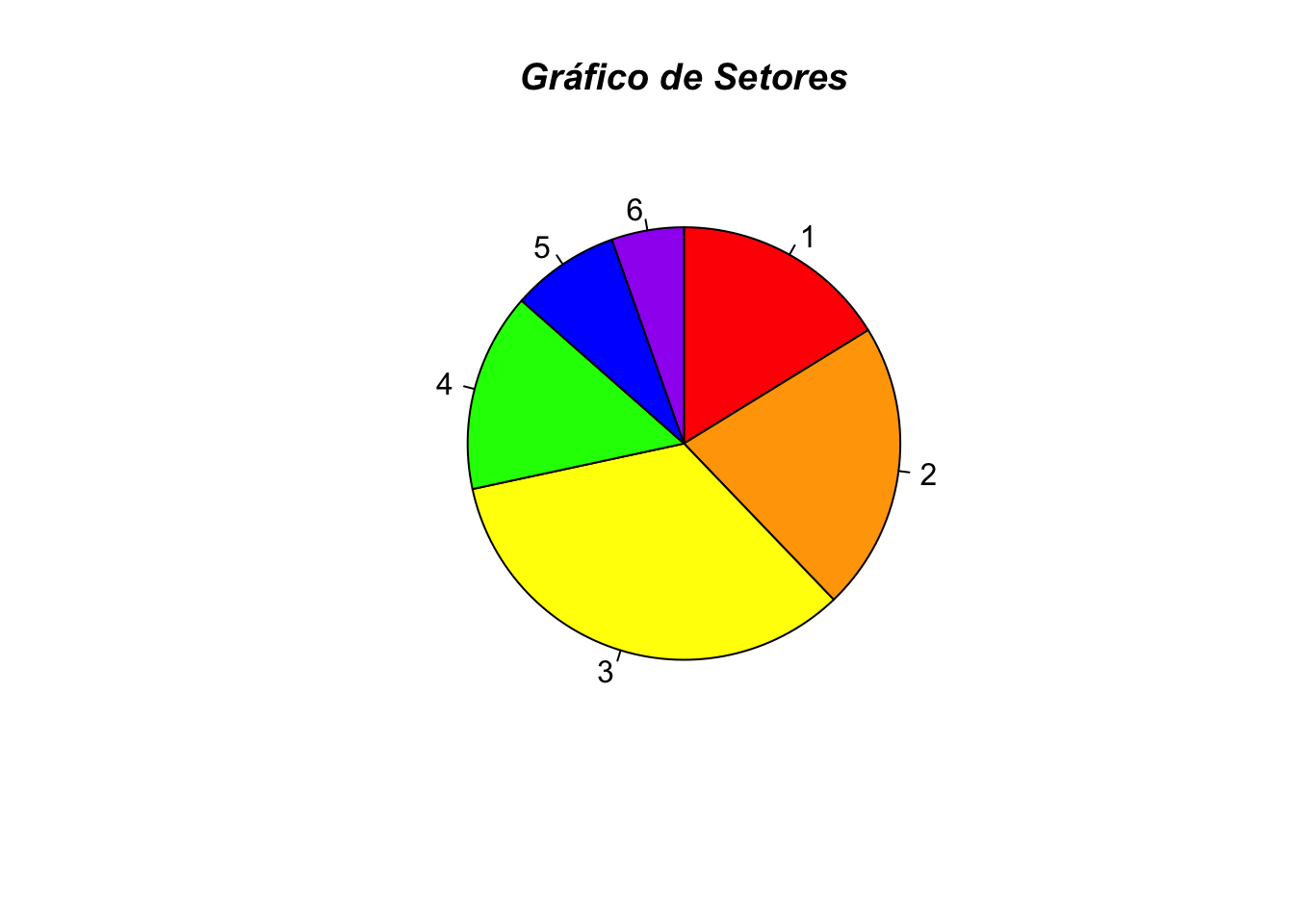

Velocidade = aaa$Velocidade
to_pie = cut(Velocidade, seq(from = 0, to = 120, by = 10))
to_pie2 = as.data.frame(table(to_pie))
to_pie2 = to_pie2[to_pie2$Freq > 0, ]
pie(to_pie2$Freq, labels = "", main="Gráfico de Setores")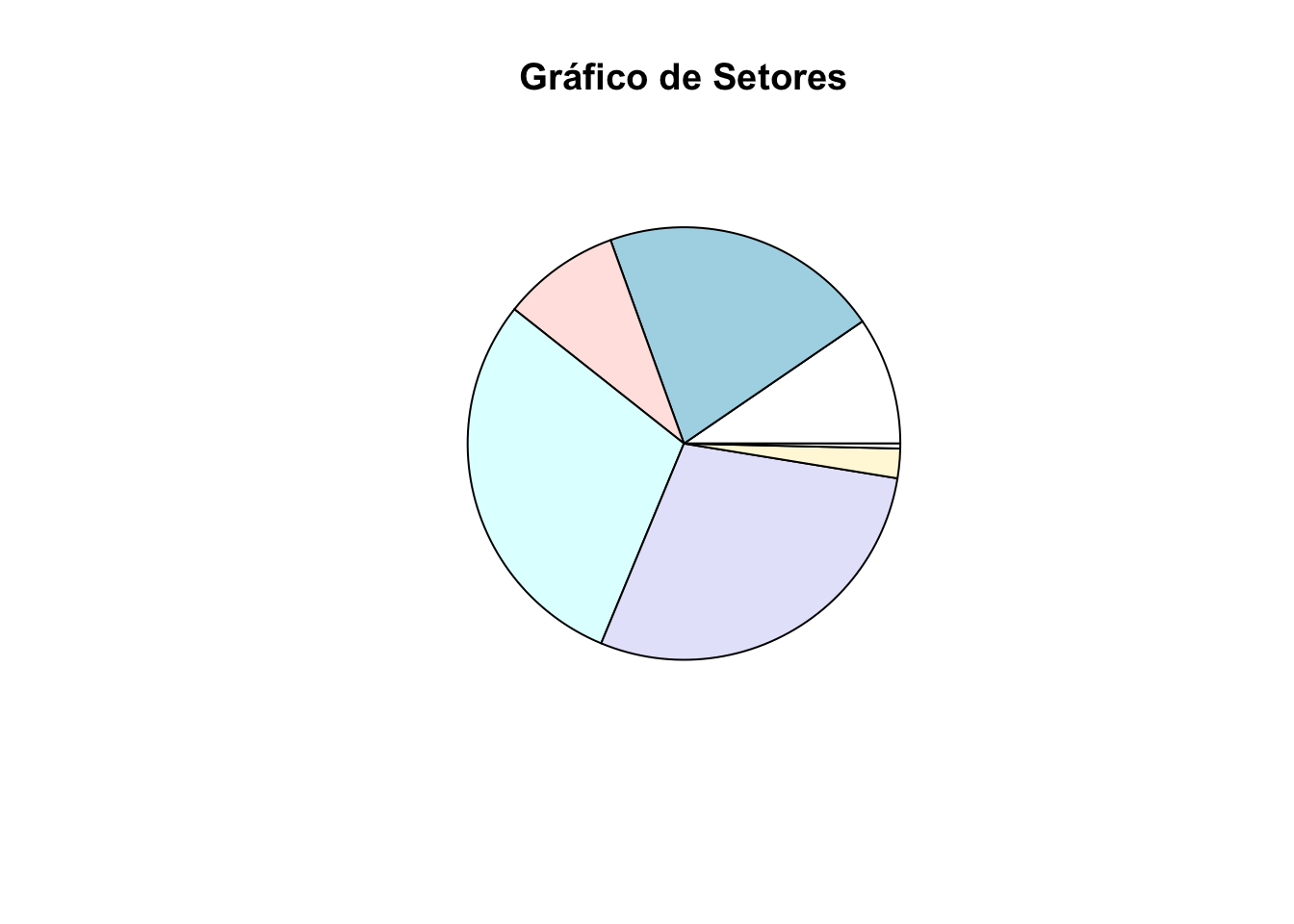

library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

library(ggplot2)
data <- data.frame(Velocidades=to_pie,b=1:length(to_pie))
head(data)

##   Velocidades b
## 1   (110,120] 1
## 2     (50,60] 2
## 3     (70,80] 3
## 4     (60,70] 4
## 5     (80,90] 5
## 6     (50,60] 6

data <- data %>% 
  group_by(Velocidades) %>% 
  count() %>% 
  ungroup() %>% 
  mutate(per=`n`/sum(`n`)) %>% 
  arrange(desc(Velocidades))
data$label <- scales::percent(data$per)

ggplot(data=data)+
  geom_bar(aes(x="Setores", y=per, fill=Velocidades), stat="identity", width = 2)+
  coord_polar("y", start=20)+
  theme_void()+
  geom_text(aes(x=1.7, y = cumsum(per) - per/2, label=label)) + ggtitle("Gráfico de Setores")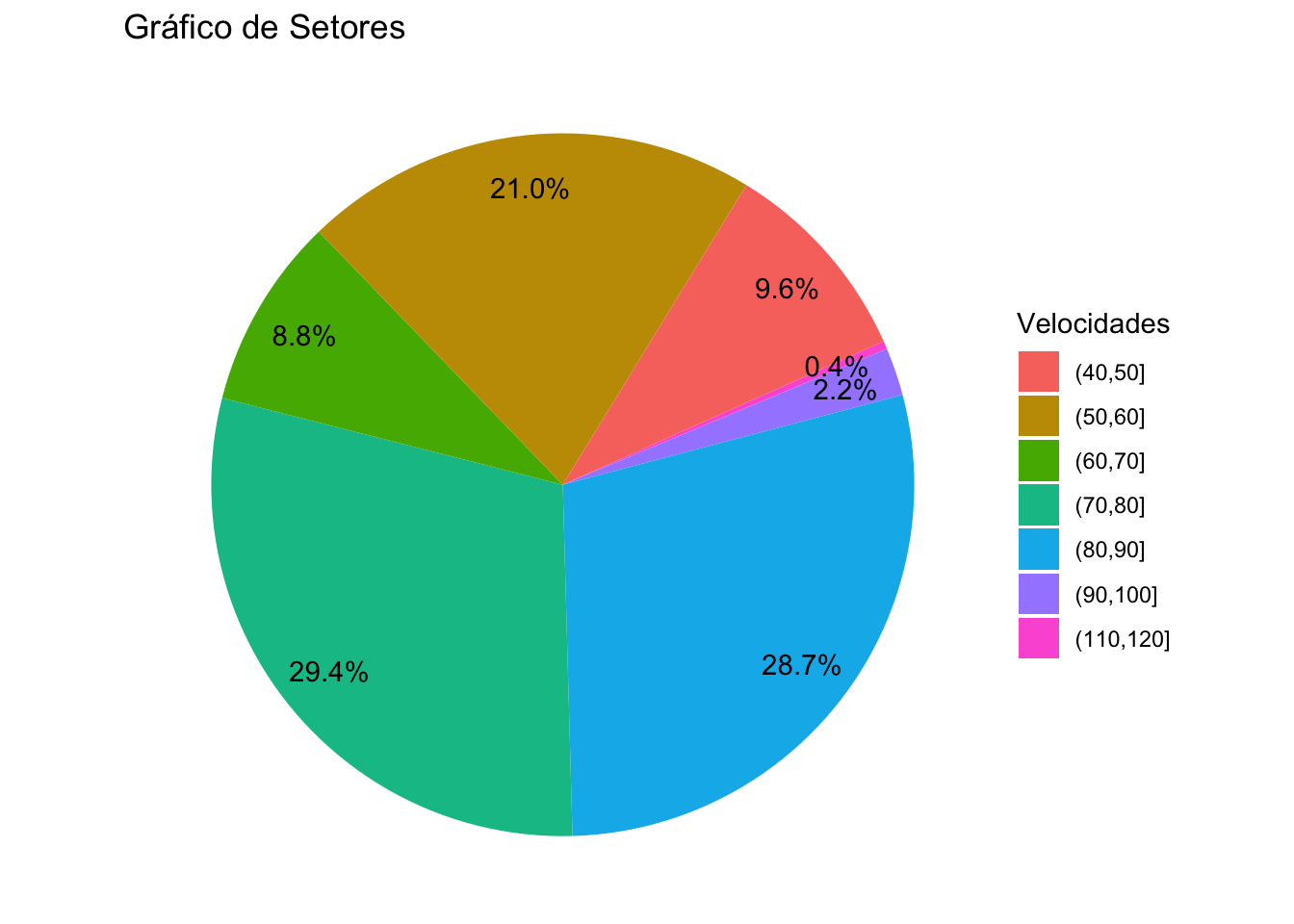 

Histogramas

Os histogramas constituem um tipo de gráfico muito semelhante ao gráfico de barras e são bastante uteis para representação de grandes conjuntos de dados. Histogramas exibem a frequência ou percentuais de valores que pertencem a certos intervalos pré-definidos. As barras de histogramas são obtidas através da densidade de frequência que pode ser obtida, através da divisão da frequência pela amplitude da classe: densidade de frequência = frequência / amplitude da classe. É importante ressaltar que o comportamento de histogramas tanto para frequências como para percentuais é o mesmo. Se forem criados dois histogramas de uma amostra representando os dados em frequência absoluta (escala numérica) e frequência relativa (percentuais) a forma do histograma permanece inalterada. Um exemplo de histograma pode ser visto na Figura 8: Histograma de Velocidades Verificadas

Velocidade = aaa$Velocidade
hist(Velocidade, ylab="Frequencia", col="#FF682D", main="Histograma de Velocidades",breaks=10 )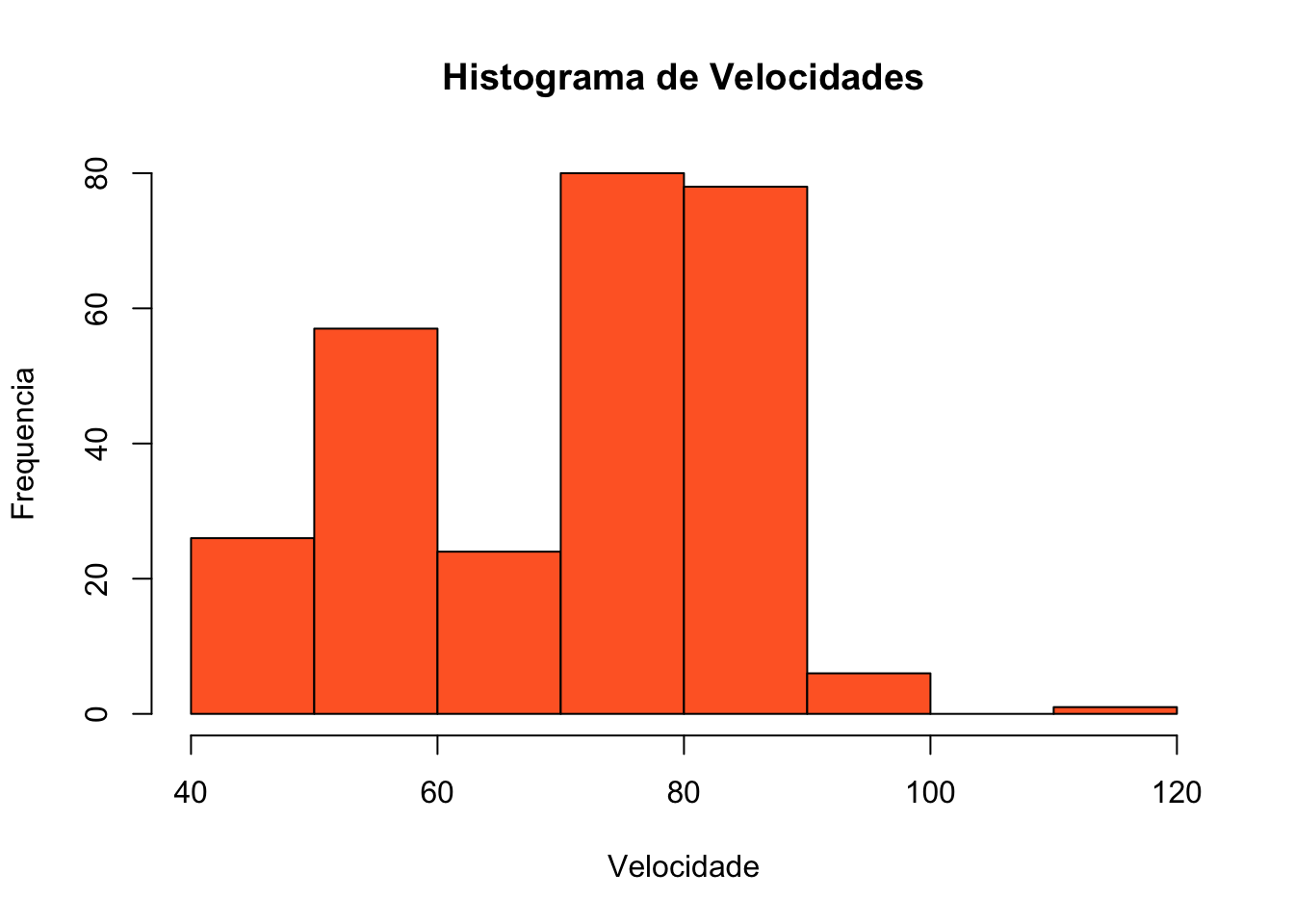

Figura 8: Histograma de Velocidades Verificadas

Uma vantagem dos histogramas é a possibilidade de criar intervalos diferentes amplitudes. Caso intervalos vizinhos possuam um desiquilíbrio em que um possua elevada frequência de casos e outro reduzida frequência de dados, é possível criar um único intervalo com uma maior amplitude alargando a base para que a barra que representa a densidade de frequência assuma um valor ajustado que possa ser representado graficamente sem prejuízo para sua visualização e interpretação. Desse modo se todas as demais densidades de frequência estiverem próximas de 500 como por exemplo 5589/10 obtemos a densidade de 558.9, mas se duas classes vizinhas possuem valores como 14852/10=1485.2 e 952/10= 95.2; uma solução de equilíbrio seria unir os dois intervalos, aumentando a amplitude e reduzindo a densidade 14852+952/20, o que resulta em uma amplitude de 790.2, mais próxima das densidades que se aproximam de 500. Esta técnica pode ser utilizada também para evitar intervalos de valores vazios; o histograma da Figura 9: Histograma Ajustado para intervalos de poucas frequências, apresenta esta solução, criando um intervalo de 90 a 120, eliminando o hiato entre 101 e 110. Em muitos casos o ultimo intervalo pode ter seu valor máximo desconhecido, o que exige estimar este valor, de modo a obter um intervalo satisfatório para gerar a densidade de frequência estimada para este intervalo. Uma vez obtidas as frequências de todos os intervalos, o histograma é criado contendo todos intervalos no eixo das abscissas e as densidades no eixo das ordenadas. Este arranjo utilizando o cálculo da densidade de frequências resulta que, em histogramas o modelo de representação de dados possui representações distintas onde, o eixo das ordenadas não representa mais as frequências e sim a área de cada bloco passa a representar as frequências.

hist(Velocidade, ylab="Frequencia", col="#FF682D", main="Histograma de Velocidades",breaks=c(40,50,60,70,80,90,120) )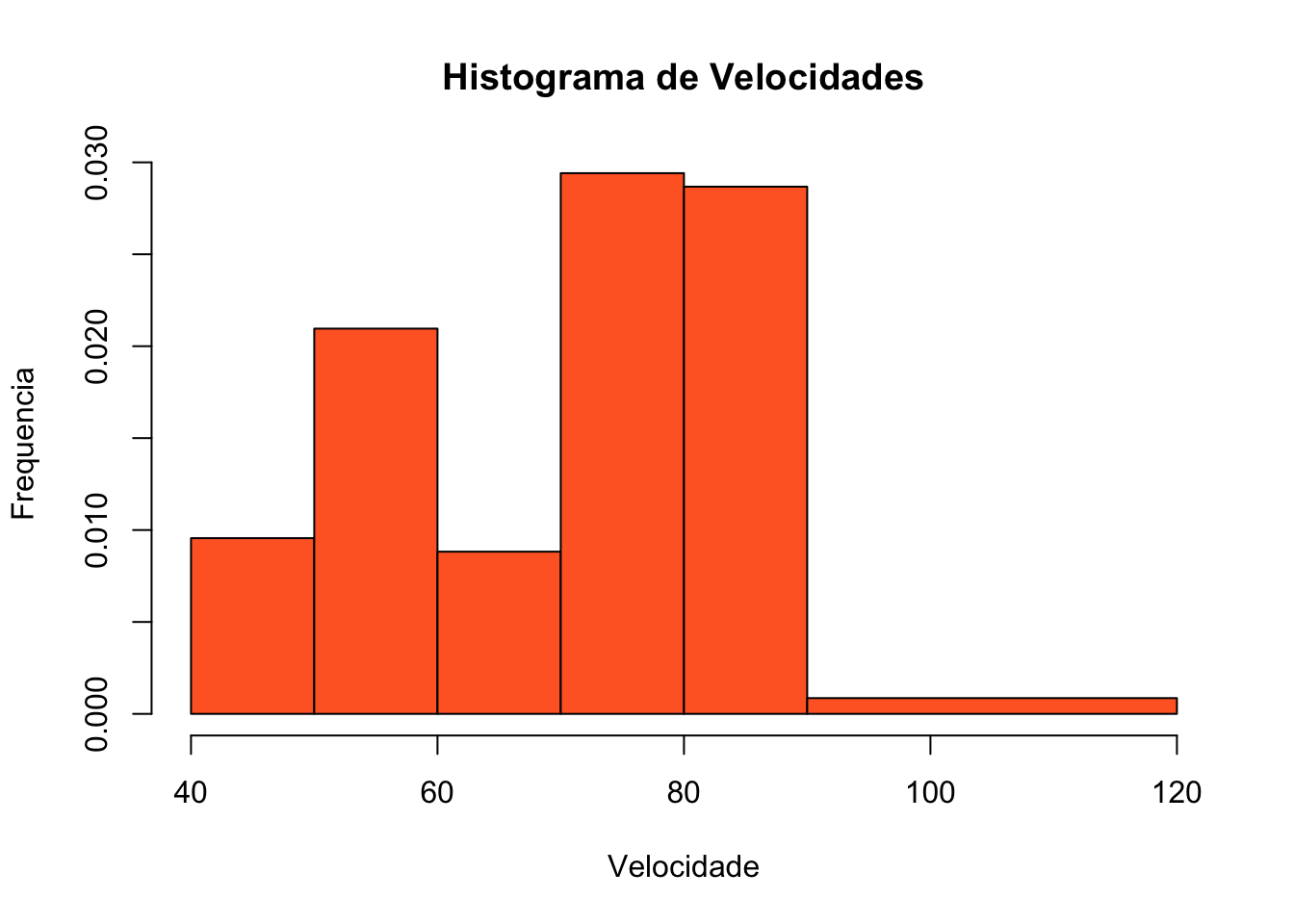

# função para obter a moda pelo método do histograma, moda obtida por
# interpolação linear, baseado em semelhaça de triângulos
moda.hist <- function(ht, plotit=TRUE){
  ## ht: um objeto do uso da função hist()
  mcl <- which.max(ht$counts)
  li <- ht$breaks[mcl]
  width <- diff(ht$breaks[mcl+0:1])
  counts <- c(0,ht$counts,0)
  delta <- abs(diff(counts[1+mcl+(-1:1)]))
  moda <- li+width*delta[1]/sum(delta)
  cols <- rep(5, length(ht$counts))
  cols[mcl] <- 3
  if(plotit==TRUE){
    plot(ht, col=cols)
    abline(v=moda)
  }
  return(moda=moda)
}

# função para obter a moda da função densidade kernel

moda.dens <- function(dn, plotit=TRUE){
  ## dn: um objeto do uso da função density()
  ini <- dn$x[which.max(dn$y)]
  fx <- approxfun(dn$x, dn$y)
  op <- optim(c(ini), fx, method="BFGS", control=list(fnscale=-1))
  if(plotit==TRUE){
    plot(dn)
    abline(v=op$par, col=2)
  }
  return(moda=op$par)
}


x <- Velocidade
ht <- hist(x, freq=FALSE, col="gray86")
mo1 <- moda.hist(ht, plotit=FALSE)
abline(v=mo1, lwd=2, col = "green")
dn <- density(x)
lines(dn, col=4, lwd=2)
mo2 <- moda.dens(dn, plotit=FALSE)
abline(v=mo2, col="pink", lwd=2)
box()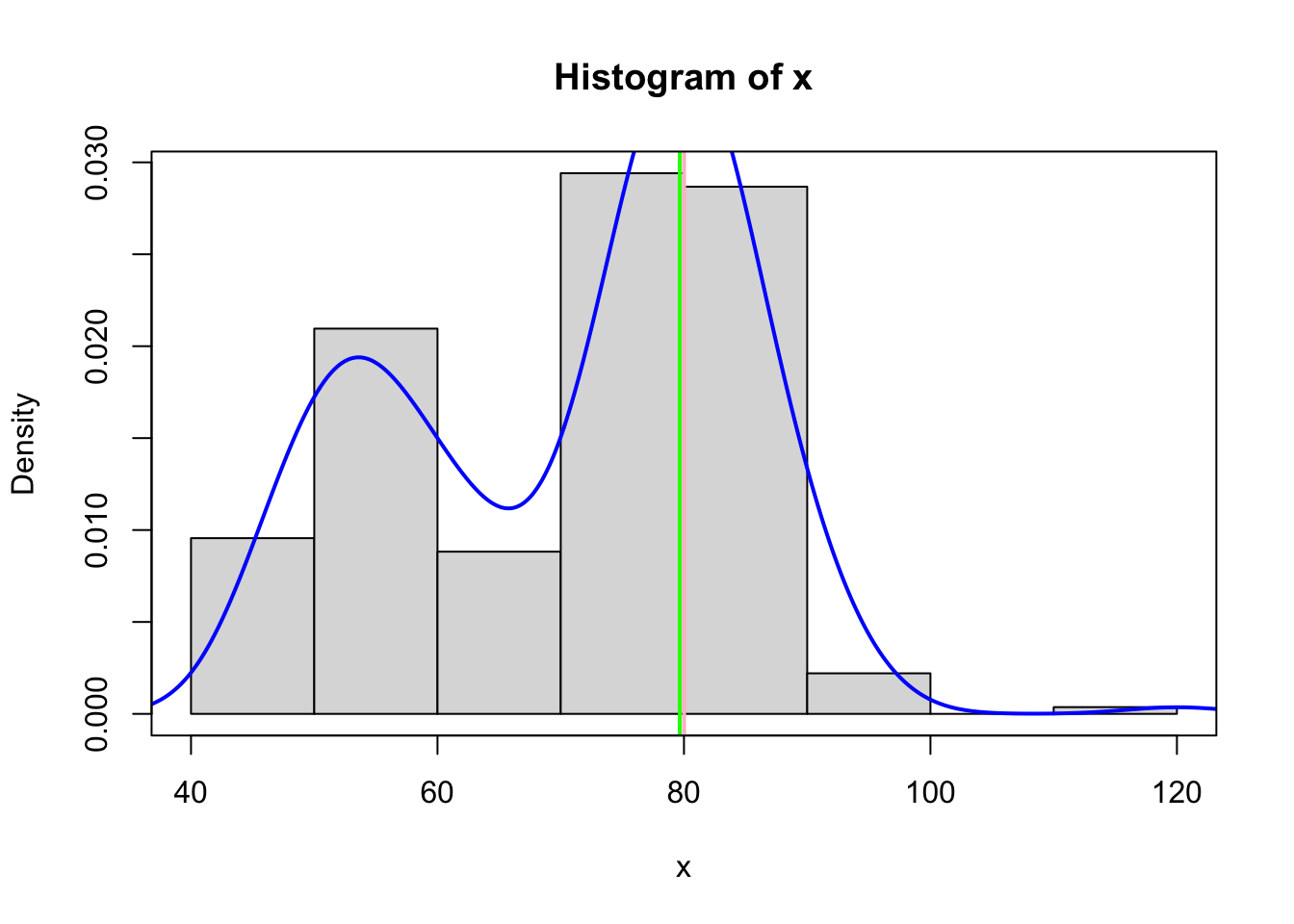

Gráfico de pontos

Este modelo de gráfico é semelhante ao modelo de ramo em folhas, mas suas peculiaridades permitem que o mesmo seja utilizado para representar também v.a. categóricas. No lugar dos valores numéricos do ramo de um gráfico de ramo e folhas, podemos ter valores categóricos. Em uma pesquisa cujo interesse é conhecer a disciplina preferida de cada aluno de uma sala de aula, o gráfico pode ser organizado a manter cada disciplina na base do gráfico e sobre cada disciplina são colocados tantos pontos quantos forem as declarações de preferência pela mesma disciplina.

library(dplyr)
library(ggplot2)
to_pie = cut(Velocidade, seq(from = 0, to = 120, by = 10))
to_pie2 = as.data.frame(table(to_pie))
to_pie2 = to_pie2[to_pie2$Freq > 0, ]
data <- data.frame(Velocidades=to_pie,b=1:length(to_pie))
ggplot(data, aes(x = Velocidade, fill = factor(Velocidade))) +
  geom_dotplot(stackgroups = TRUE, binwidth = 1, method = "histodot")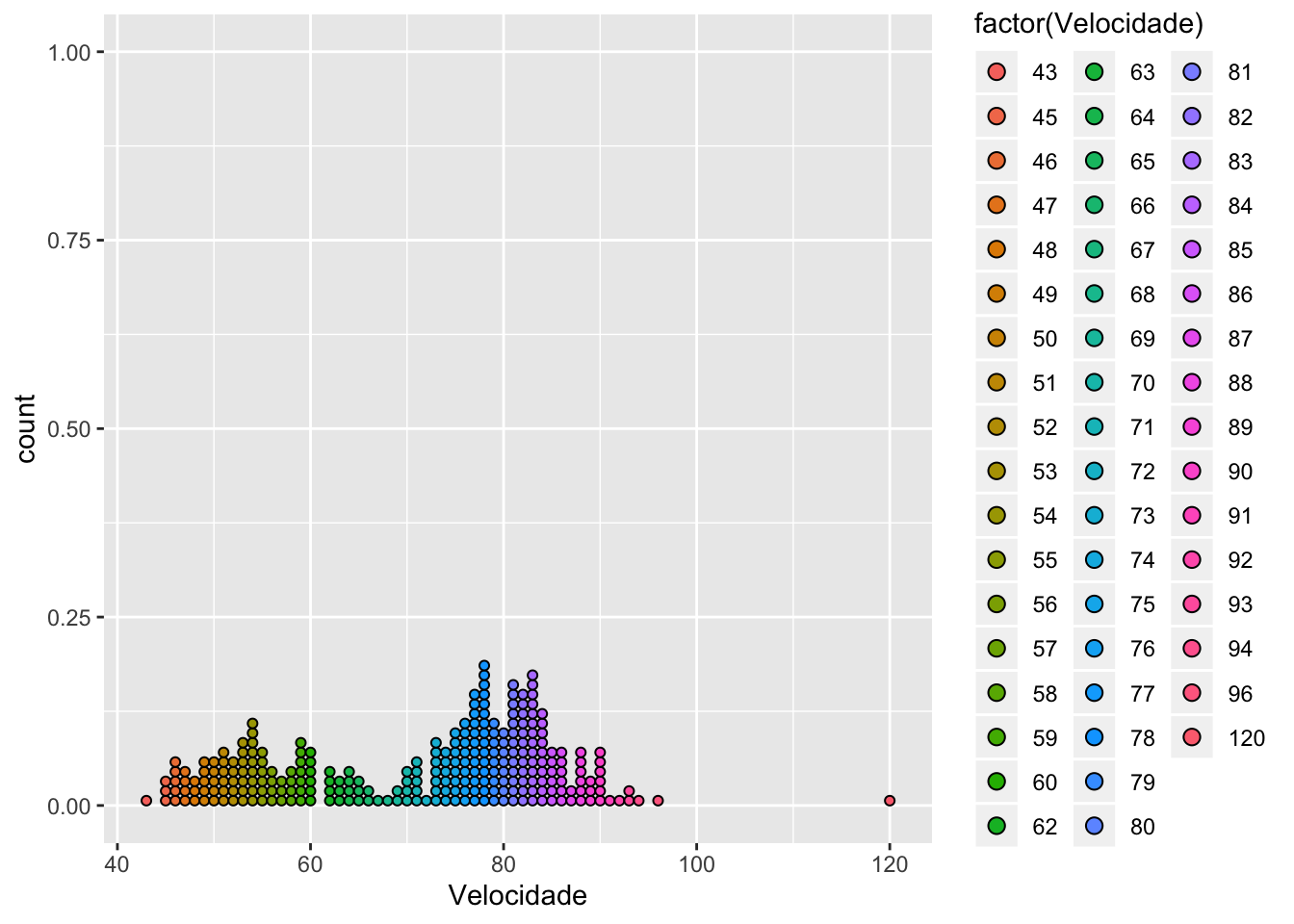

ggplot(mtcars, aes(x = mpg, fill = factor(cyl))) +
  geom_dotplot(stackgroups = TRUE, binwidth = 1, method = "histodot")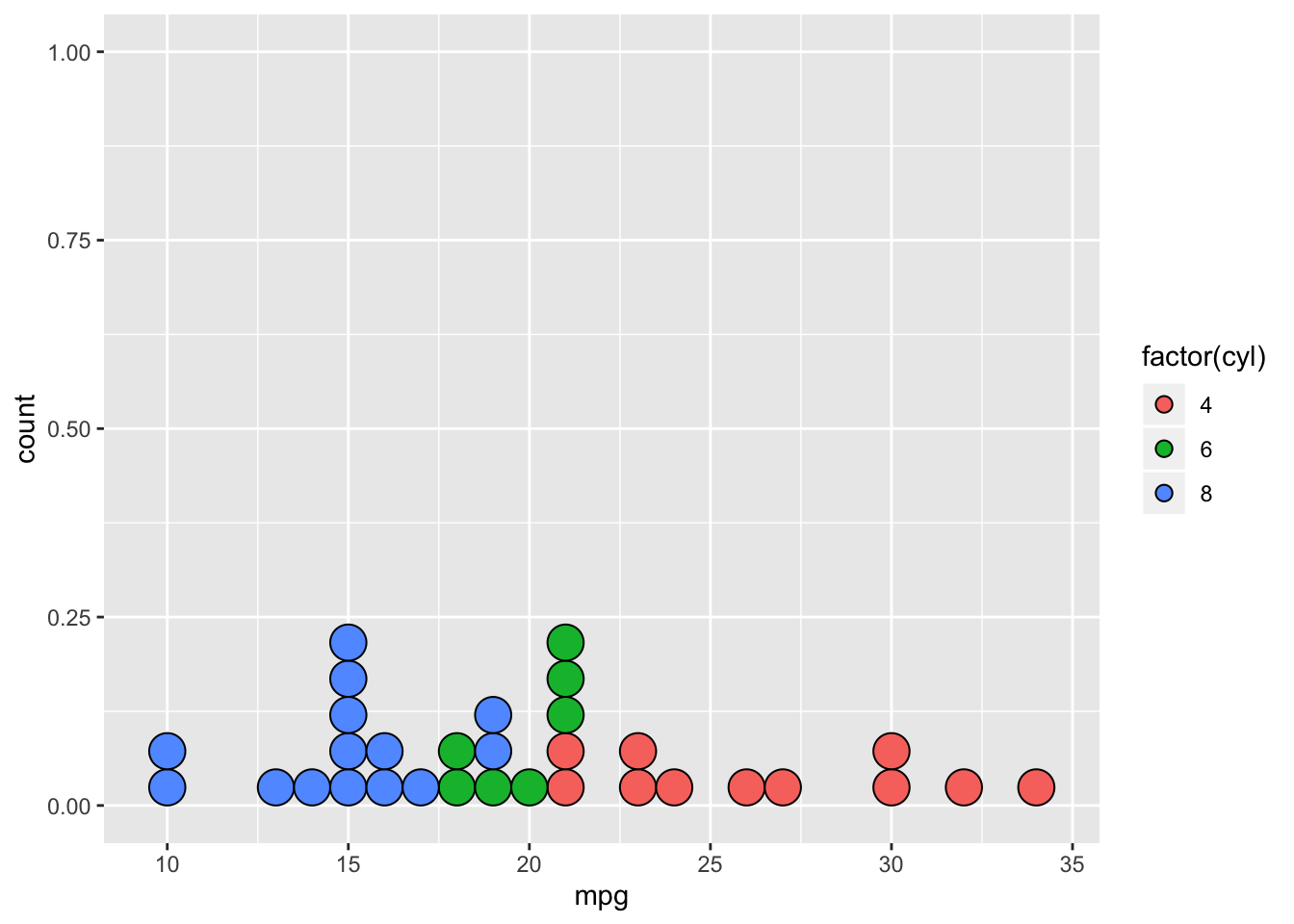

Gráfico de Modas

Alguns gráficos possuem uma ou mais picos que representam os valores que apresentam maiores ocorrências. Estes valores com maior frequência de ocorrências são chamados de moda. As v.a. que possuem mais de uma moda podem ser classificados como bimodais ou multimodais, a depender do número de modas verificadas. Nem todo pico pode ser considerado uma moda, para efeitos práticos, podemos considerar como moda todo pico que apresenta mudanças significativas na forma gráfica da distribuição.

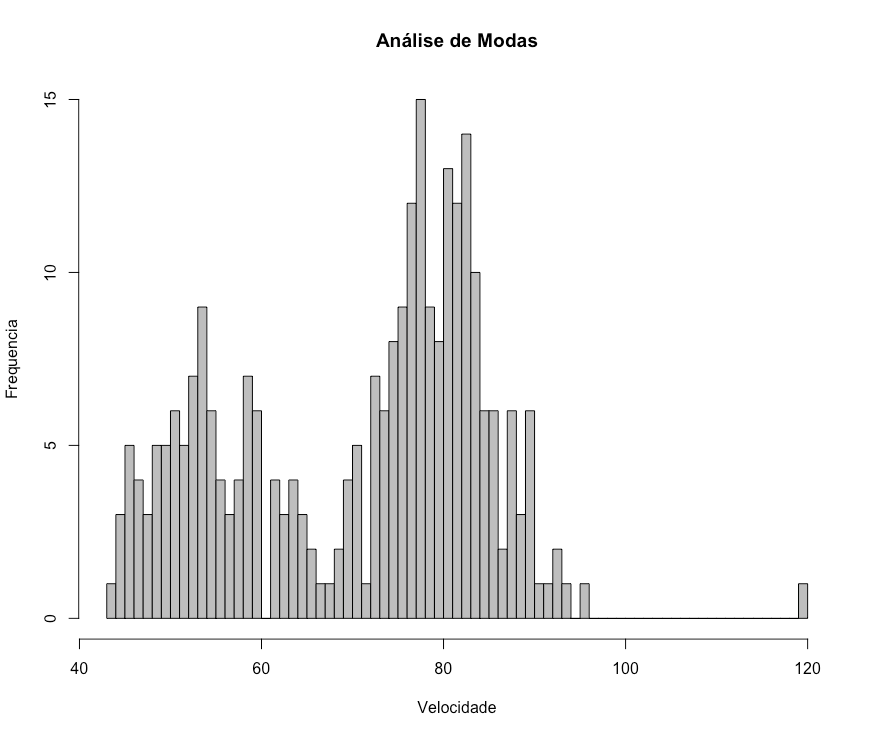
Figura 11: Gráfico Bimodal

Boxplots

Alguns tipos de medidas resumo contidas no presente trabalho são de suma importância para identificar padrões de distribuição de dados. São valores uteis em uma analise os valores máximo e mínimo, a média, a mediana e os quartis. O gráfico boxplot é um tipo de gráfico utilizado justamente para apresentar estas medidas. O mesmo é útil para demonstrar a amplitude de uma v.a. também é útil para identificar Outliers. Um gráfico de boxplot constitui-se de um retângulo que representa os 50% dos dados ao centro da distribuição. Além desse retângulo este tipo de gráfico possui dois prolongamentos que partem das extremidades do retângulo, também chamados de bigodes chamados de limite inferior e superior, que correspondem à mediana menos 1.5 vezes o intervalo entre o 1º e o 3º quartil da v.a. de uma lado e a mediana mais 1.5 vezes o intervalo entre o 1º e o 3º quartil da v.a. de outro. Os valores contidos no prolongamento das arestas são denominados valores adjacentes e aqueles dados que extrapolam estas arestas são considerados outliers ou valores atípicos. Pelo exposto e pela figura…. Podemos verificar que o boxplot é um gráfico que permite identificar se uma v.a. possui distribuição simétrica ou assimétrica. O boxplot também fornece claramente por meio de recursos visuais a identificação das medidas de posição e dispersão. A primeira extremidade do retângulo corresponde ao primeiro quartil ou a posição que possui 25% dos dados abaixo dela e a segunda extremidade corresponde ao terceiro quartil ou posição que mantem 75% dos dados abaixo dela. No centro de retângulo há uma terceira linha que representa a mediana ou segundo quartil. O segundo quartil pode estar no centro do retângulo ou mais próximo da posição do primeiro ou terceiro quartil. Quando o valor da mediana se aproxima do 1º ou 3º quartil identificamos uma assimetria da distribuição; portando identificamos que os dados não seguem uma distribuição normal. Se nosso boxplot apresenta a mediana, ou 2º quartil muito próximo do 1º quartil temos uma assimetria à direita, significando uma assimetria para os valores máximos; de outro modo, quando boxplot apresenta a mediana, ou 2º quartil muito próximo do 3º quartil temos uma assimetria à esquerda, significando uma assimetria para os valores mínimos. Os boxplots podem ser uteis para identificar outliers que podem ser resultado de valores atípicos, erros de mensuração ou de registro, o que oferece subsídios para auditar os dados para identificar qual das três hipóteses acima ocorre (BUSSAB; MORETTIN, 2017).

  boxplot(aaa$Velocidade,main="Boxplot de Velocidades", 
        xlab="Velocidades Verificadas",horizontal = TRUE, col = "#0196A7")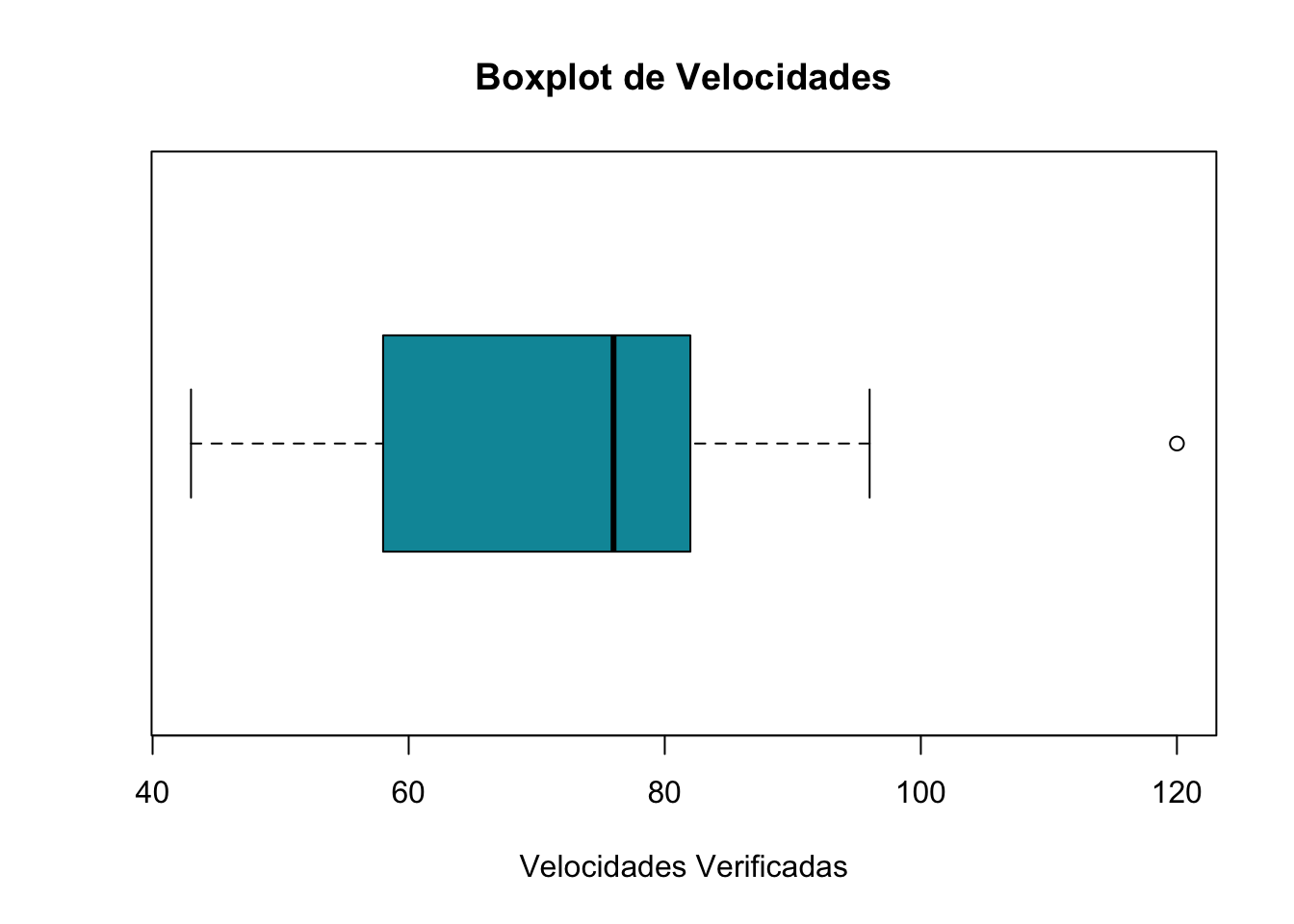

Figura 12: Gráfico de Boxplot

Gráficos de Dispersão

  plot(aaa$Velocidade, aaa$Veiculos, xlab="Velocidade", ylab="Potencia", main = "Gráfico de dispersão" ,pch=19, col="#513C69") 
abline(lm(aaa$Veiculos ~aaa$Velocidade), col="red", lwd=5, lty=2)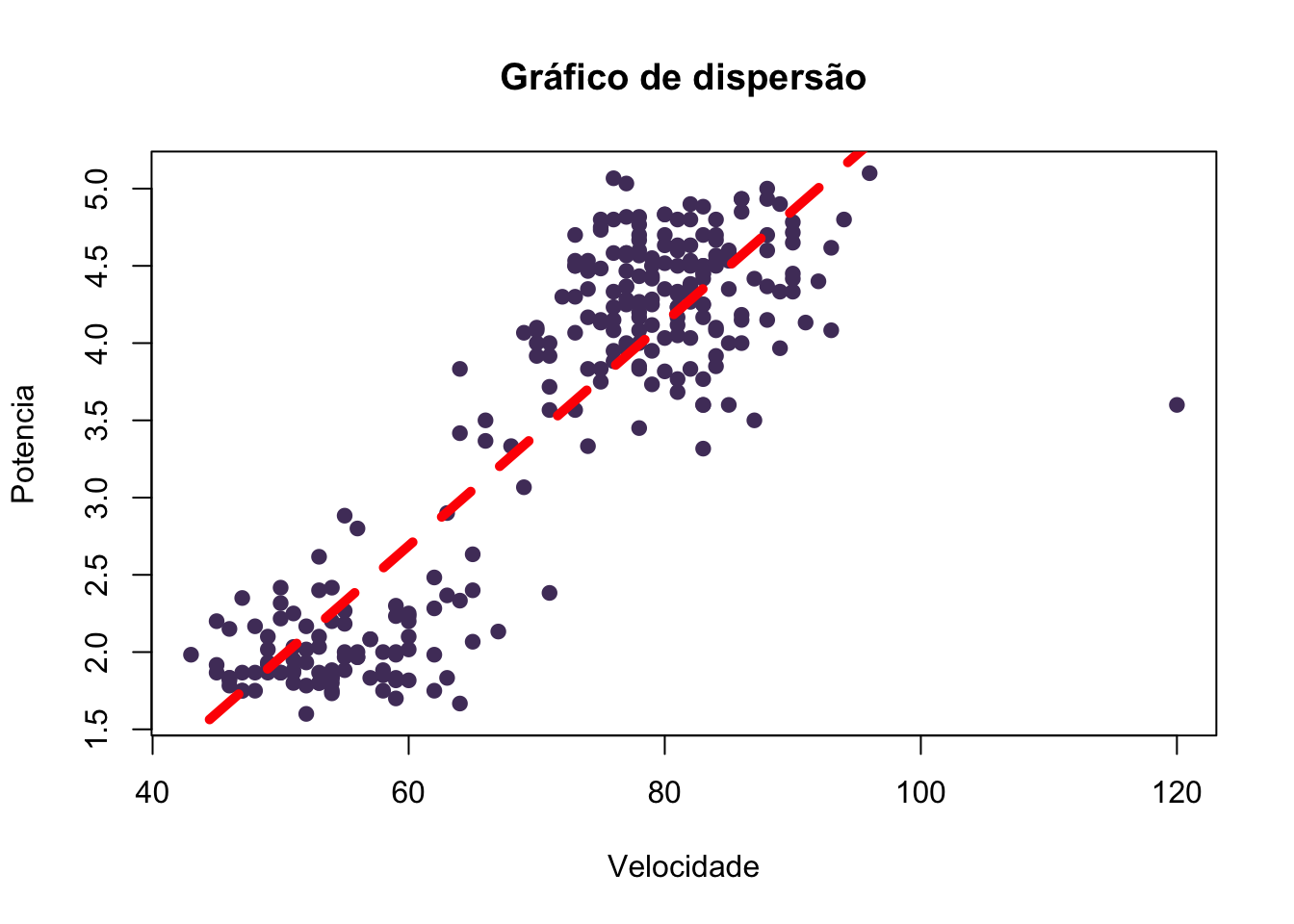

Figura 13: Gráfico de Dispersão

Gráficos de Frequência Acumulada

Também conhecidos como gráficos de ogiva ou polígonos de frequência, os gráficos de frequência acumulada, representam a cada ponto os valores do intervalo atual acrescido dos demais que o precedem (DOWNING; CLARK, 2002). Os gráficos de distribuição acumulada performam linhas que exibem o somatório das frequências acumuladas no eixo das ordenadas (Y) a medida que acompanham os intervalos de classe nas abscissas (X). Os gráficos de distribuição acumulada tem seus pontos de computo alinhados ao que seria o canto direito dos histogramas; dado que, como a linha delineia a soma das frequências, ela atualiza seu valor ao término da enumeração de todas as v.a. de cada intervalo de classe. Os gráficos de distribuição acumulada também servem para explicar a obliquidade de um conjunto amostral como será melhor detalhado nos Gráficos de Forma. Brevemente pode-se demonstrar conforme apresentado na figura Figura 14: Gráfico de Frequência Acumulada, que quando um gráfico de frequência acumulada inicia com inclinação suave da linha de frequências, este gráfico constitui uma distribuição de inclinação negativa; quando a linha inicia com uma curva bastante íngreme, tem-se uma distribuição com inclinação positiva; naqueles casos em que o gráfico apresenta uma linha em formato sigmoide, esta linha representa uma distribuição normal, e por fim, nos casos de distribuições multimodais a linha de frequências acumuladas não apresenta uma forma típica, mas associada à aleatoriedade dos picos modais.

set.seed(1234)                            
n = 1000;  x1 = rbeta(n, .5, .4)
y1 = rnorm(n, 5, 2);  y2 = rnorm(n, 10, 1)
w = rbinom(n, 1, .5)                      
x2a = w*y1 + (1-w)*y2                     
par(mfrow=c(2,2))
hist(rbeta(10000,5,2), col="#0196A7", main="Inclinação Negativa")
hist(rbeta(10000,2,5), col="#0196A7", main="Inclinação Positiva")
hist(rbeta(10000,5,5), col="#0196A7", main="Normal")
hist(x2a, col="#0196A7", main="Bimodal")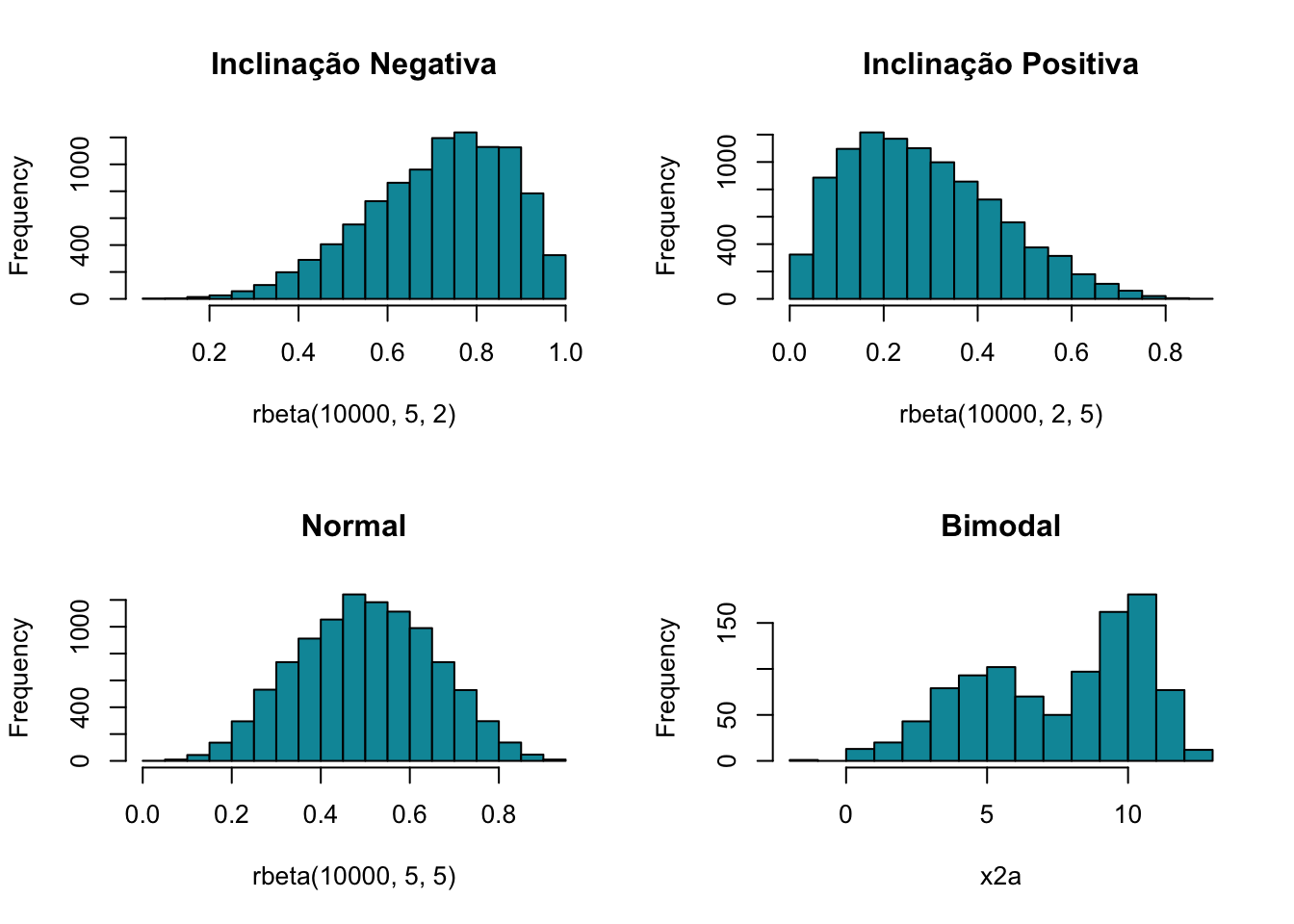

Figura 14: Gráficos de Frequência Acumulada

par(mfrow=c(2,2))
x1 = rbeta(10000,5,2)
x1 = x1 * 20
head(x1)

## [1] 15.620915 16.858184  6.764383 11.389840 19.529805 15.309261

hist(x1, 
     xlim=c(min(x1),max(x1)), probability=T, nclass=max(x1)-min(x1)+1, 
     col='#0196A7', xlab=' ', ylab=' ', axes=F,
     main='Inclinação Negativa')
lines(density(x1,bw=1), col='#513D69', lwd=3)

x2 = rbeta(10000,2,5)
x2 = x2 * 20
hist(x2, 
     xlim=c(min(x2),max(x2)), probability=T, nclass=max(x2)-min(x2)+1, 
     col='#FFA000', xlab=' ', ylab=' ', axes=F,
     main='Inclinação Positiva')
lines(density(x2,bw=1), col='#513D69', lwd=3)

x3 = rbeta(10000,5,5)
x3 = x3 * 20
hist(x3, 
     xlim=c(min(x3),max(x3)), probability=T, nclass=max(x3)-min(x3)+1, 
     col='#FFA000', xlab=' ', ylab=' ', axes=F,
     main='Curva Normal')
lines(density(x3,bw=1), col='#513D69', lwd=3)

hist(x2a, 
     xlim=c(min(x2a),max(x2a)), probability=T, nclass=max(x2a)-min(x2a)+1, 
     col='#FFA000', xlab=' ', ylab=' ', axes=F,
     main='Distribuição Bimodal')
lines(density(x2a,bw=1), col='#513D69', lwd=3)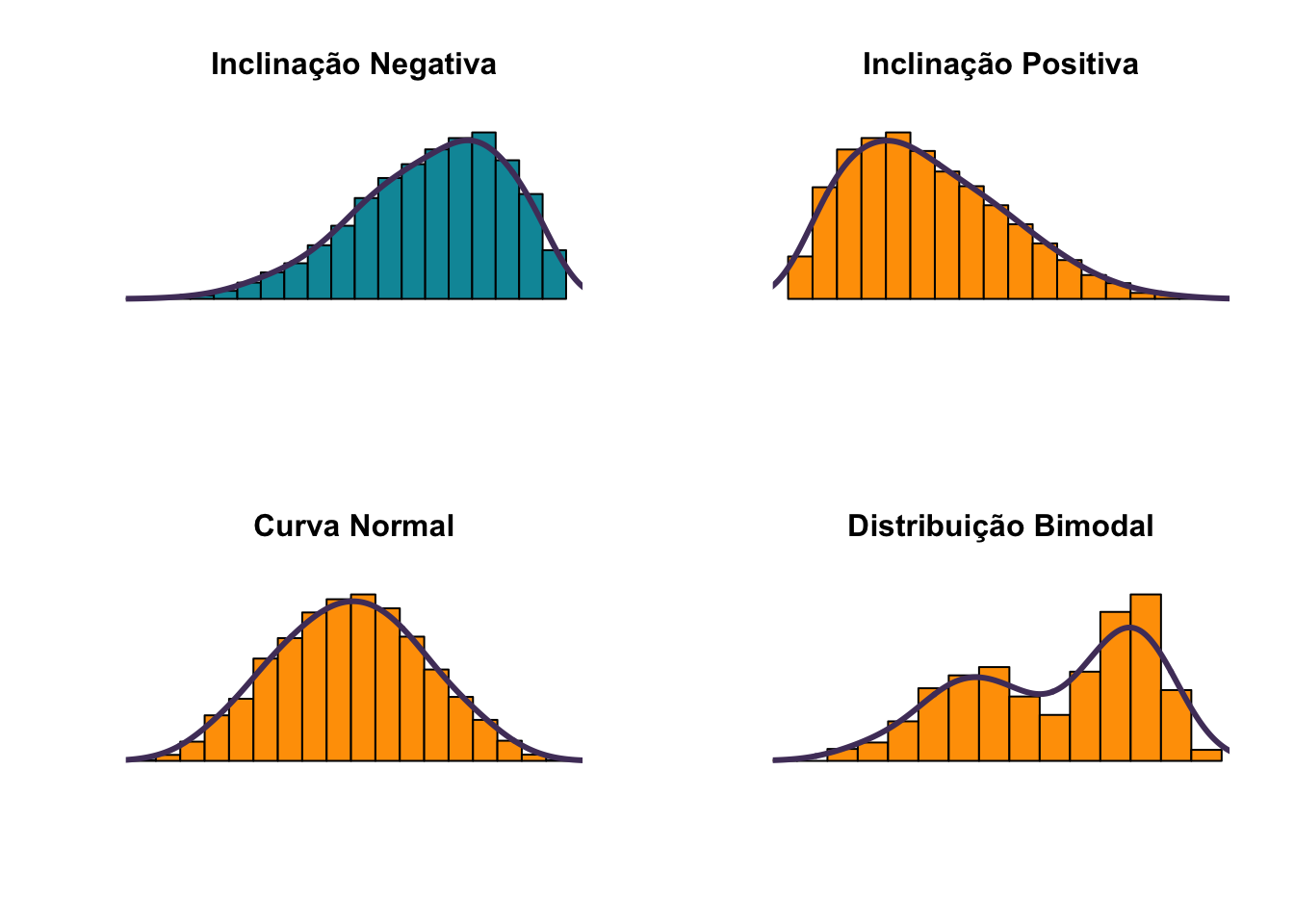

Gráficos de Forma

Quando são utilizados gráficos de frequência, de ramo e folhas e histogramas, uma utilidade desses modelos de gráficos é a visualização da forma da distribuição. Algumas distribuições possuem formatos típicos que podem dizer muito sobre elas, mesmo antes de acessarmos os valores de frequências e medidas de resumo (WITTE; WITTE, 2010).

par(mfrow=c(2,2))

x <- x1
hcum <- h <- hist(x, plot=FALSE)
hcum$counts <- cumsum(hcum$counts)
plot(hcum, ylab="Frequencia Acumulada", xlab="Intervalos de Classe", border="white", main="Distribuição com Inclinação à Esquerda")
plot(h, add=T, col="grey")

## Plot the density and cumulative density
d <- density(x)
lines(x = d$x, y = d$y * length(x) * diff(h$breaks)[1], col="#30BACB", lwd = 3)
lines(x = d$x, y = cumsum(d$y)/max(cumsum(d$y)) * length(x), col="#FF682D", lwd = 3)

x <- x2
## Calculate and plot the two histograms
hcum <- h <- hist(x, plot=FALSE)
hcum$counts <- cumsum(hcum$counts)
plot(hcum, ylab="Frequencia Acumulada", xlab="Intervalos de Classe", border="white", main="Distribuição com Inclinação à Direita")
plot(h, add=T, col="grey")
## Plot the density and cumulative density
d <- density(x)
lines(x = d$x, y = d$y * length(x) * diff(h$breaks)[1], col="#30BACB", lwd = 3)
lines(x = d$x, y = cumsum(d$y)/max(cumsum(d$y)) * length(x), col="#FF682D", lwd = 3)

x <- x3
## Calculate and plot the two histograms
hcum <- h <- hist(x, plot=FALSE)
hcum$counts <- cumsum(hcum$counts)
plot(hcum, ylab="Frequencia Acumulada", xlab="Intervalos de Classe", border="white", main="Distribuição Normal")
plot(h, add=T, col="grey")
## Plot the density and cumulative density
d <- density(x)
lines(x = d$x, y = d$y * length(x) * diff(h$breaks)[1], col="#30BACB",  lwd = 3)
lines(x = d$x, y = cumsum(d$y)/max(cumsum(d$y)) * length(x), col="#FF682D",   lwd = 3)


x <- x2a
## Calculate and plot the two histograms
hcum <- h <- hist(x, plot=FALSE)
hcum$counts <- cumsum(hcum$counts)
plot(hcum, ylab="Frequencia Acumulada", xlab="Intervalos de Classe", border="white", main="Distribuição Bimodal")
plot(h, add=T, col="grey")
## Plot the density and cumulative density
d <- density(x)
lines(x = d$x, y = d$y * length(x) * diff(h$breaks)[1], col="#30BACB", lwd = 3)
lines(x = d$x, y = cumsum(d$y)/max(cumsum(d$y)) * length(x), col="#FF682D", lwd = 3)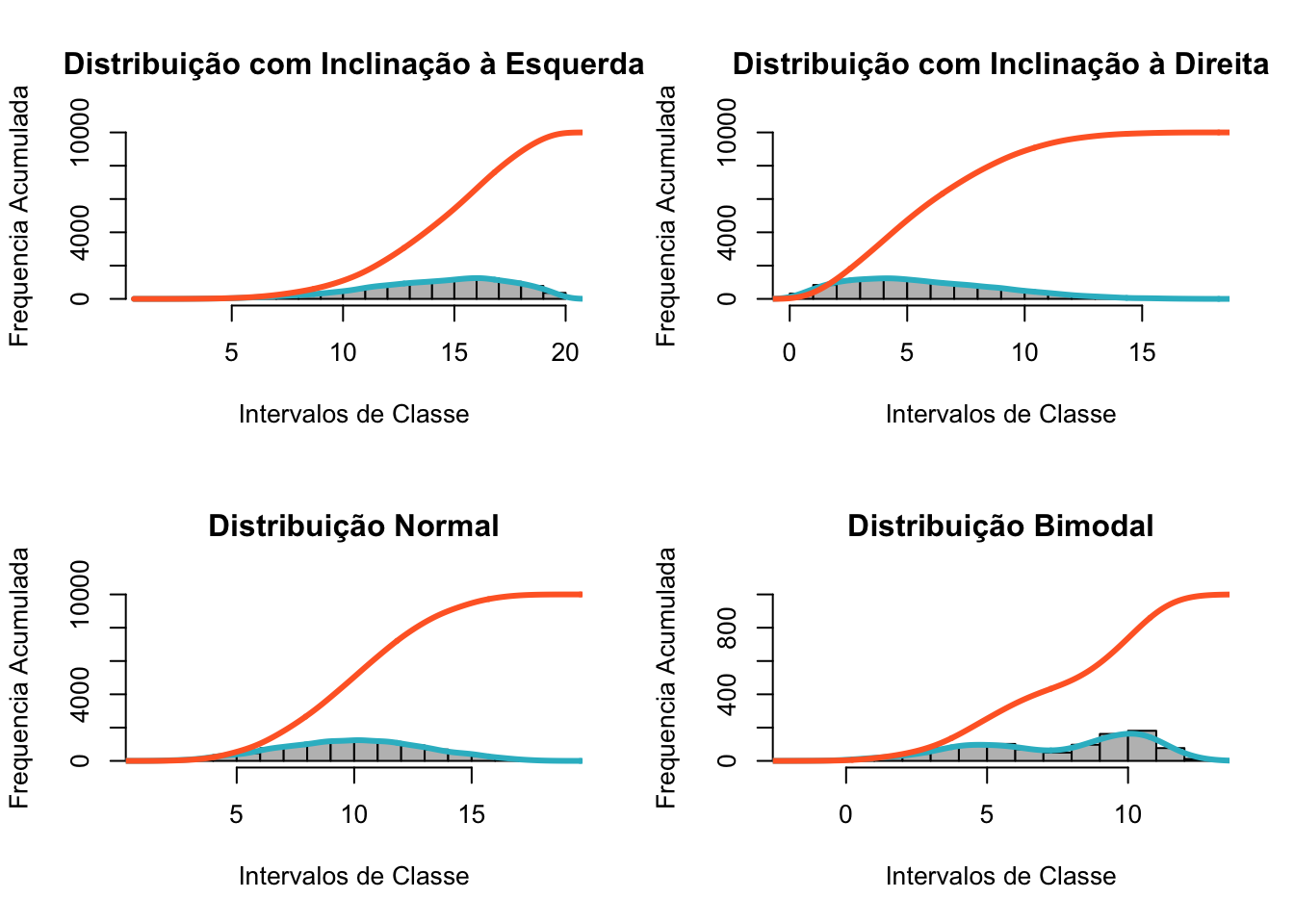

x <- Velocidade
hcum <- h <- hist(x, plot=FALSE)
hcum$counts <- cumsum(hcum$counts)
plot(hcum, ylab="Densidade", xlab="Velocidades", main="Gráfico de Distribuição Acumulada")
plot(h, add=T, col="#0195A6")

d <- density(x)
lines(x = d$x, y = d$y * length(x) * diff(h$breaks)[1], col="#FF682D", type="o", lwd = 3)
lines(x = d$x, y = cumsum(d$y)/max(cumsum(d$y)) * length(x), col="#513C69",  type="b", lwd = 3)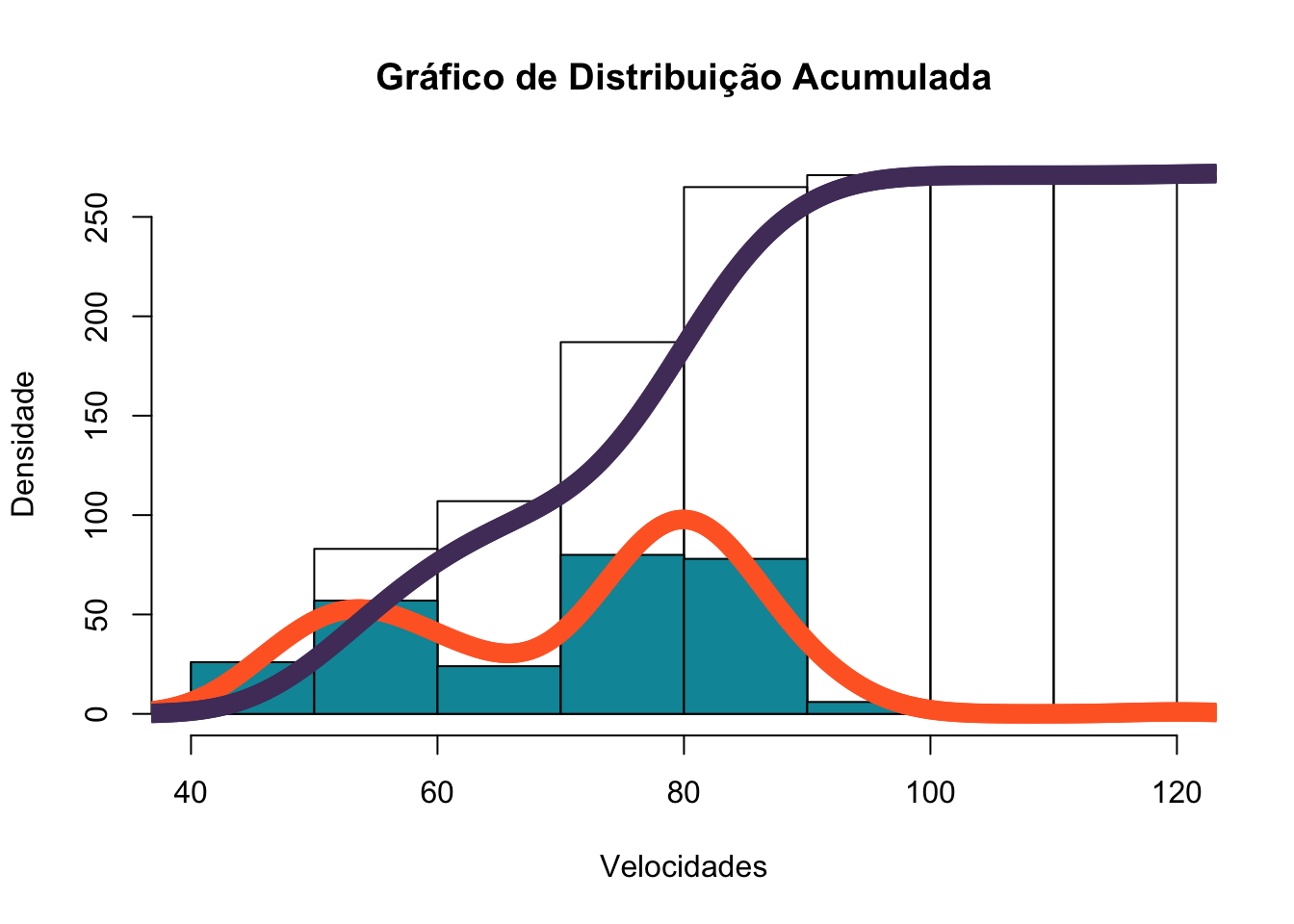

Figura 15: Gráficos de Forma e sua Distribuição Acumulada

Os gráficos de forma nos permitem identificar certos padrões e nos adiantam sugestões para elaborarmos hipóteses quando lidamos com análise exploratória de dados. Os gráficos de forma também são chamados de gráficos de simetria, pois permitem identificar quando as distribuições são simétricas, aproximadamente simétricas ou assimétricas; o conceito de simetria será esclarecido no tópico que trata de Distribuição Normal. Os gráficos da Figura 16: Histogramas com Linhas de Densidade Estimadas, apontam quatro formas típicas de gráficos que nos falam muito sobre a distribuição de dados. O primeiro gráfico nos mostra uma distribuição de inclinação negativa, onde uns poucos dados extremos se localizam na direção negativa. Gráficos de assimetria negativa possuem um único pico, onde a moda representa a maior frequência absoluta, que coincide com o pico, com seu valor sendo superior à média e mediana; que pode ser representado esquematicamente da seguinte forma: Media < Mediana < Moda (CONTI, 2011). O segundo gráfico apresenta inclinação positiva onde apenas algumas poucas observações extremas se encontram na direção à direita ou positiva. Os gráficos de assimetria positiva tamém possuem um único pico, com caso a moda representando a maior frequência absoluta, que coincide com o pico, mas, inversamente aos gráficos inclinação negativa, o valor da moda ou pico tem seu valor inferior à média e mediana; que pode ser representado esquematicamente da seguinte forma: Moda < Mediana < Média.

Os gráficos de inclinação positiva e negativa, se caracterizam pela assimetria ou obliquidade, significando que as distribuições não são uniformes. O terceiro gráfico apresenta distribuição normal e, portanto, é unimodal, enquanto que o último possui distribuição bimodal. Os gráficos de distribuição normal são simétricos, e, portanto, os dois primeiros quartis se constituem como identidade do terceiro e quarto quartis, onde a média, a mediana e a moda são muito próximas ou mesmo se sobrepõem. Já quando falamos de gráficos multimodais estes gráficos não são simétricos e possuem formatos diversos, tornando pouco recomendável a tentativa de identificação da direção da assimetria dos mesmos, a não ser por meio de coeficientes de assimetria capazes de identificar as assimetrias que constituem o conjunto de dados. Nos casos de gráficos multimodais as posições da media, modas e mediana não possuem um padrão definido de uma em relação as demais, justamente porque as assimetrias são particulares ao número de modas identificadas em cada amostra. É importante notar que quando um gráfico possui inclinação positiva, ou negativa o conceito pode ser enganoso; por exemplo, um gráfico de inclinação positiva na realidade possui a maior parte de seus dados concentrados na direção oposta, a inclinação positiva significa dizer que alguns dados fogem do que seria a curva normal apresentando valores extremos superiores à média do conjunto de dados da v.a. em análise. Os gráficos de inclinação positiva são gráficos com uma forma assimétrica, com a cauda alongada à direita em relação a posição da cauda da esquerda, identificando a presença de valores superiores extremos; como exemplo, imagine a população de alunos de uma escola de ensino fundamental, onde as idades variam entre 5 e 13 anos, é possível que alunos que entraram atrasados na escola ou que repetiram de ano inúmeras vezes ainda frequentem a mesma escola, assim poderiam ser identificados alguns casos de alunos com 15 ou 16 anos, gerando essa inclinação positiva à direita. Assim como os gráficos de inclinação positiva, os gráficos de inclinação negativa apresentam o mesmo comportamento, invertendo apenas a direção da inclinação. Um exemplo de um gráfico de inclinação negativa, poderia ser a população de alunos de uma universidade de ponta. Onde a população de alunos estaria em um intervalo de 17 a 22 anos, mas que poderia contar com alguns poucos alunos super dotados que ingressaram na universidade com 13 ou 14 anos, esses poucos casos estenderiam a base do gráfico no sentido do limite inferior, representando a existência de alguns valores registrados abaixo do intervalo que compreende a maioria das frequências de idade enumeradas. Gráficos de forma normal, ou unimodal, são os mais comuns; visto o que diz a lei do teorema central; onde quanto maior a amostra de uma v.a. a tendência é que a forma do gráfico assuma a forma de um sino, com a moda ao centro de distribuição, aproximada da média, e as bordas sendo suavizadas para esquerda e direita compreendendo a amplitude determinada pelo menores e maiores valores da v.a. em análise. Gráficos unimodais e de distribuição normal são simétricos, onde uma metade do gráfico se apresenta como reflexo da outra. De outro modo para gráficos unimodais normais, podemos considerar a média como a bissetriz que separa duas partes semelhantes. Como exemplo de um gráfico unimodal podemos considerar o gráfico que toma o tempo de viagem de um veículo de uma cidade Porto Alegre até a cidade de Novo Hamburgo; via de regra os veículos levam aproximadamente o mesmo tempo percorrendo um mesmo trajeto, então a maioria dos tempos obtidos se aproxima da média, gerando frequências relativas de tempo concentradas em torno da média e poucos tempos registrados que se afastam da média; representando veículos que levaram muito mais ou muito menos tempo até o destino final. O exemplo abaixo da curva normal constitui uma representação clara desse fenômeno, onde a maioria dos carros leva quase o mesmo tempo, com altas frequências verificadas próximas ao centro de gráfico, e raros casos à direita e esquerda, representando aqueles veículos mais apressados ou mais lentos.

Gráficos bimodais ou multimodais resultam de distribuições amostrais com mais de uma moda, em que dois ou mais intervalos apresentam frequências relativas superiores às demais e distantes em relação às dispersões da v.a. da amostragem. Tomando o mesmo exemplo do trajeto entre as cidades de Porto Alegre e Novo Hamburgo; se considerarmos o tempo médio dos veículos no mesmo trajeto tomando amostras realizadas em dias úteis e em finais de semana, é bem provável que tenhamos duas modas e, portanto, um formato de gráfico bimodal. Esse fenômeno ocorre porque há uma alta frequência de veículos que levam um tempo X1 para percorrer o mesmo trajeto em dias uteis em função do acentuado tráfego de veículos e um segundo grupo de veículos que possui uma frequência significativa, que levam um tempo X2 para percorrer o mesmo trajeto; visto que, por se tratarem de veículos conduzidos aos finais de semana, com menor fluxo de veículos, na ausência de congestionamentos, há uma tendência de realizar a viagem em menor espaço de tempo. Uma outra abordagem interessante quando se utiliza gráficos de formas, seja por meio de histogramas ou por meio de linhas de densidade estimadas permitem identificar clusters e gaps. Atualmente a análise de clusters é uma técnica muito utilizada em estatística, ciência de dados, machine learning e etc. quando uma distribuição apresenta forma multimodal, esta é uma forte candidata a ser tomada como uma distribuição de uma v.a. que pode ser analisada por meio de clusters. Os clusters são subgrupos naturalmente definidos, que representam conjuntos de dados próximos que possuem alguma afinidade. Quando se fala de clusters por afinidade, isso deve ser entendido pelo comportamento de subgrupos de dados que possuem uma concentração em algum ponto da escala de valores, onde esta afinidade não se dá apenas pela acumulação dos valores em um certo ponto, pois se assim fosse, toda moda seria um cluster. Na verdade, clusters são subgrupos de dados agrupados cada um num dado intervalo, em que estes subgrupos se formam em função de outros elementos que geram a afinidade entre os mesmos. Suponha uma distribuição multimodal que representa o número de veículos em circulação, digamos que esta amostra possua três modas que representam três clusters, digamos que há uma moda no período entre 07:30 e 08:30 da manhã, uma segunda moda entre as 11:30 e 13:30 e um terceiro cluster entre as 17:30 e 19:00h. estes três clusters possuem uma concentração em três pontos bem delimitados da escala horária; onde a afinidade entre os registros da v.a. pela manhã é a concentração de veículos se deslocando de casa para o trabalho; o segundo cluster representa o grupo de veículos que se desloca no intervalo do meio-dia para ira restaurantes ou acessar algum serviço ou comercio durante este período; já o terceiro cluster representa o conjunto de veículos que se desloca do trabalho para casa, faculdade, clubes, happy hour, etc. Pelo exemplo exposto, é possível verificar que a mesma v.a. pode apresentar diversos clusters ou modas, cada um resultando de uma situação afim de define este comportamento em cada intervalo. Entre um cluster e outro podemos ter os gaps, que representam aqueles intervalos com pouca ou nenhuma frequência, estes momentos da distribuição da v.a. podem também ser chamados de entre picos, representando aqueles momentos de frequências moderadas frente aos picos que representam os clusters. Pode-se entender os gaps como os momentos moderados da v.a. constituinte da amostra.um exemplo de gráfico de forma multimodal é o gráfico da doença de Huntington, esta doença quando apresentada em um gráfico de ocorrências por idade apresenta três picos ou modas. O primeiro pico apresenta-se no intervalo de pessoas menores de 18 anos, um segundo pico entre pessoas na faixa de 35 a 45 anos e um terceiro pico na faixa de pessoas acima dos 80 anos. Este cenário apresenta três clusters representados pelos três picos citados, em que estas frequências podem ser clusterizadas por afinidade clínica, como a ocorrência de doença de Huntington Juvenil, a ocorrência de Huntington em idade adulta e a incidência da doença de Huntington em idosos, muito idosos. Para cada um dos três grupos alguns aspectos clínicos diferem e são específicos para cada faixa etária, o que constitui a afinidade em cada faixa; assim entende-se que estas altas frequências em três momentos da vida não são mero acaso, mas aspectos clínicos relevantes.

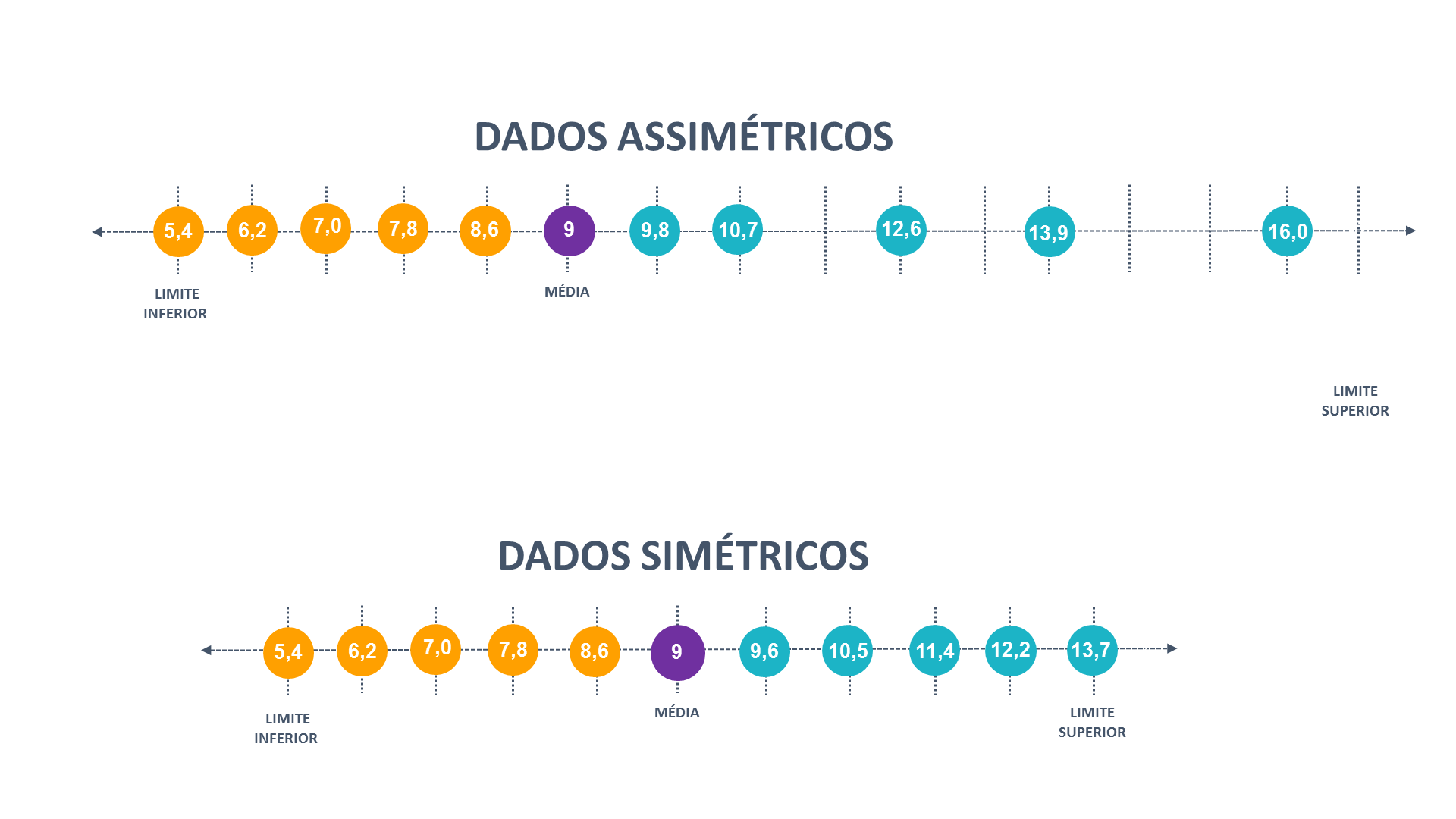
Figura 16: Disposição de dados Assimétricos e Simétricos

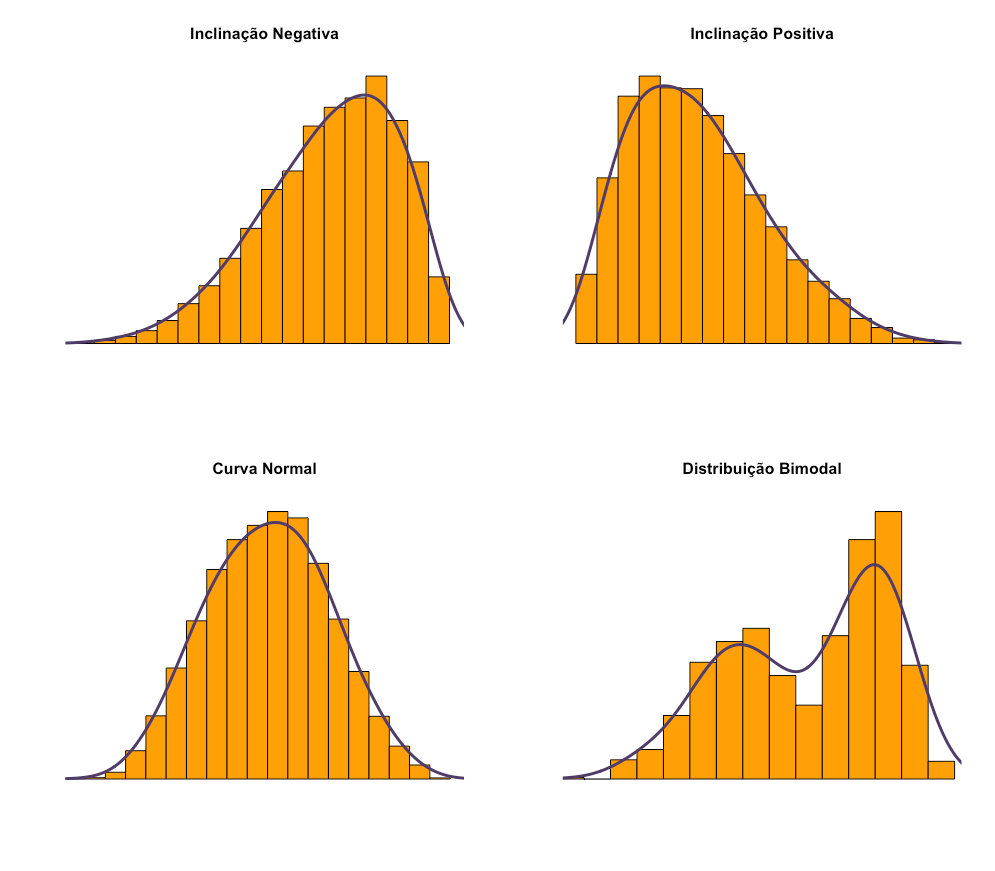
Figura 17: Histogramas com Linhas de Densidade Estimadas

Velocidade = aaa$Velocidade
d <- density(Velocidade) # returns the density data 
plot(d, main="Gráfico de Densidade", sub="", ylab="Densidade",  xlab="Velocidades") # plots the results
polygon(d, col="#0195A6")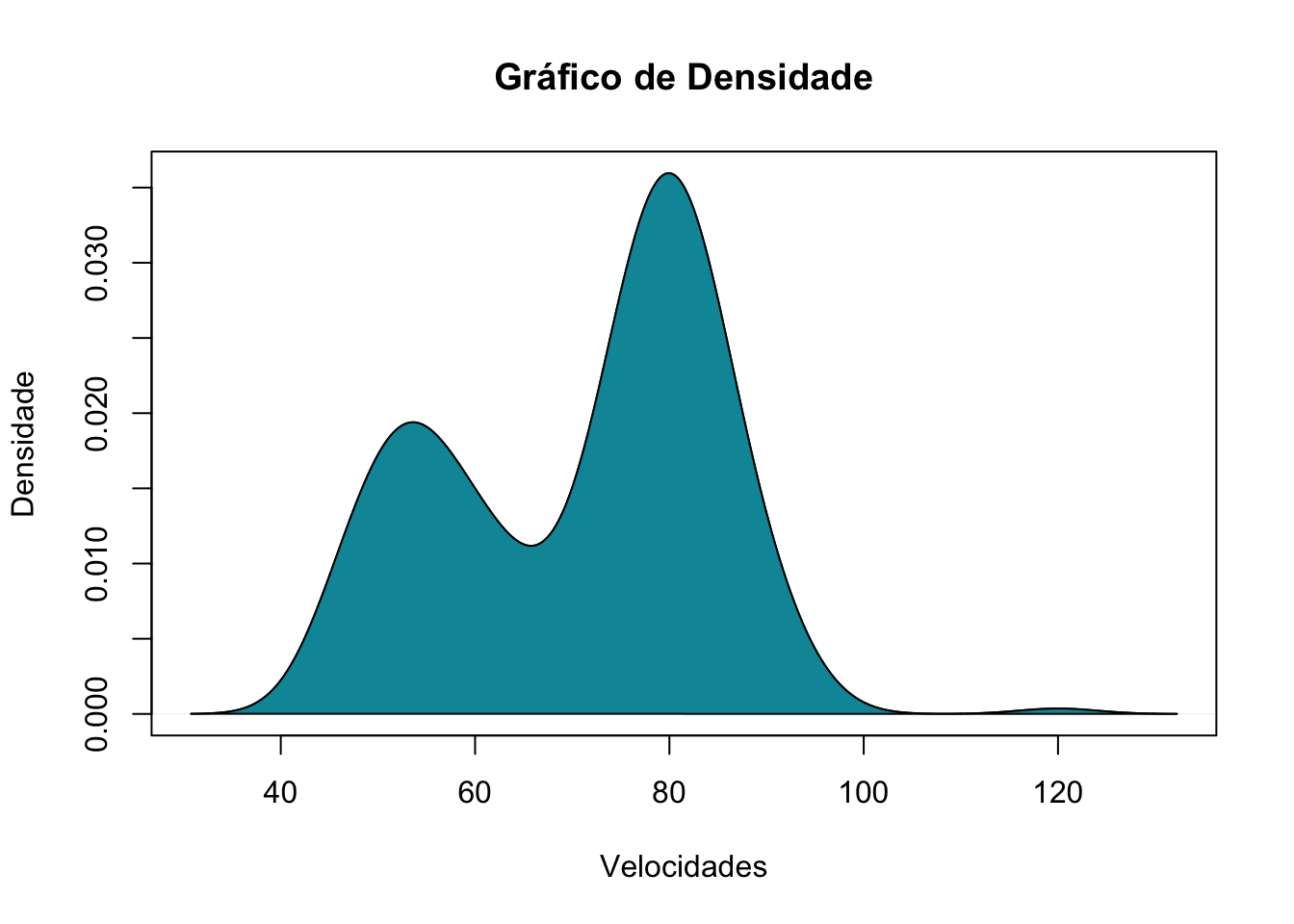

Figura 18: Gráfico de Densidade

Gráfico de Frequência

Os gráficos de frequência, também chamados de polígonos de frequência são gráficos formados por linhas que ligam os valores das frequências de cada classe. Este tipo de gráfico enfatiza a continuidade das variáveis (WITTE; WITTE, 2010), sem utilizar a suavização da inclinação, como ocorre com gráficos como o de densidade uma vez que a linha do polígono parte em linha reta de um ponto médio a outro de cada classe (DOWNING; CLARK, 2002), como pode ser visto na Figura 18: Gráfico de Polígono de Frequências.

  library(plyr)

## ------------------------------------------------------------------------------

## You have loaded plyr after dplyr - this is likely to cause problems.
## If you need functions from both plyr and dplyr, please load plyr first, then dplyr:
## library(plyr); library(dplyr)

## ------------------------------------------------------------------------------

## 
## Attaching package: 'plyr'

## The following objects are masked from 'package:dplyr':
## 
##     arrange, count, desc, failwith, id, mutate, rename, summarise,
##     summarize

data <- as.integer(round_any(aaa$Velocidade, 5, f = ceiling))
data = aaa$Velocidade
range(data)

## [1]  43 120

class_width = seq(40, 120, by=10)
class_width

## [1]  40  50  60  70  80  90 100 110 120

data.cut = cut(data, class_width, right=FALSE)
data.freq = table(data.cut)
cbind(data.freq)

##           data.freq
## [40,50)          21
## [50,60)          56
## [60,70)          26
## [70,80)          76
## [80,90)          80
## [90,100)         12
## [100,110)         0
## [110,120)         0

data.freq

## data.cut
##   [40,50)   [50,60)   [60,70)   [70,80)   [80,90)  [90,100) [100,110) [110,120) 
##        21        56        26        76        80        12         0         0

hist(data, 
     breaks=class_width, 
     col="slategray3", 
     border = "dodgerblue4",
     right=FALSE,
     xlab = "Velocidades", 
     main = "Frequencias")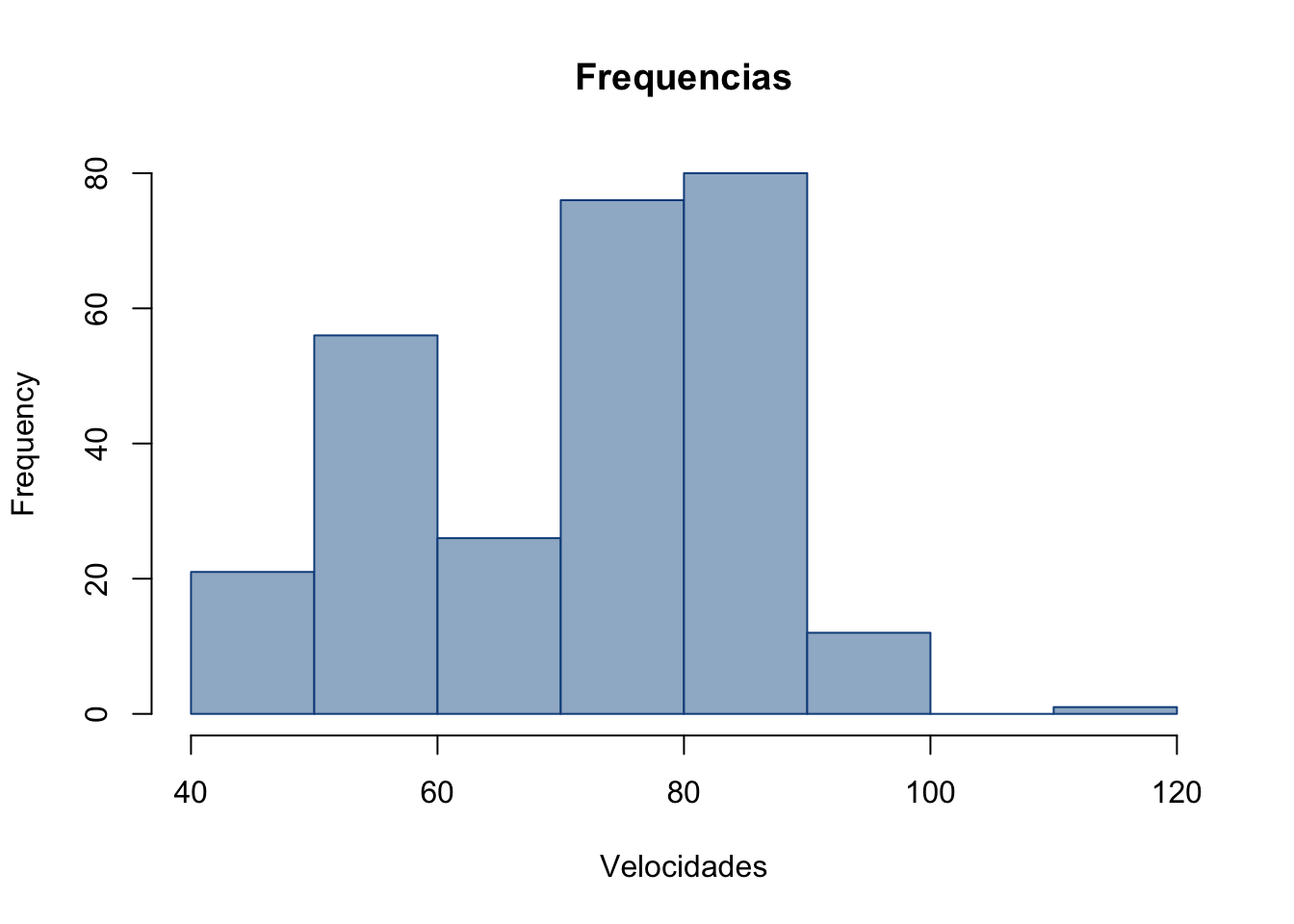

Figura 19: Gráfico Polígono de Frequências

plot(data.freq, type="b", main = "Polígono de Frequência", xlab = "Faixas de Velocidade", 
       ylab = "Frequencias", col="#513C69", pch=20,cex=2)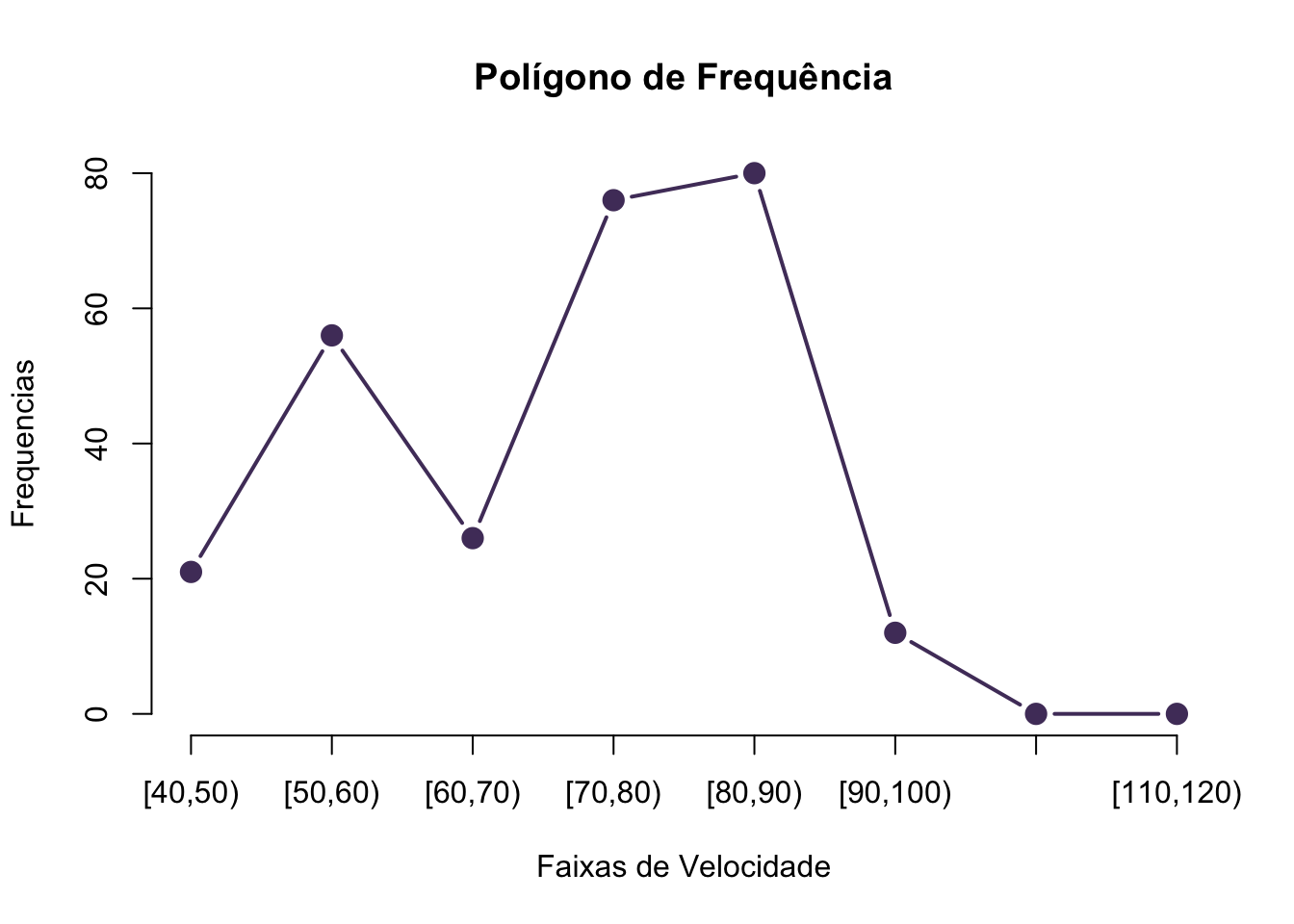

Figura 19: Gráfico Polígono de Frequências

Dados Tabulares

Dentre as alternativas para apresentar dados, o uso de tabelas representa a técnica de apresentação de dados mais comum, justamente porque as ferramentas, surgidas a partir dos anos 1960 (PAARSCH; GOLYAEV, 2016), permitem criar tabelas para apresentação de dados são diversas, de fácil manuseio e operacionalização. Para fins de resumo e apresentação de proporções ou apresentação de pares ordenados as tabelas são ferramentas recomendáveis. Dados tabulares são alternativas para representação de arrays e matrizes. Os arrays, também denominados como vetores, são considerados estruturas de armazenamento de dados de mesmo tipo. Para fins estatísticos, pode-se considerar um array como um conjunto de dados de mesmo tipo, a diferença de um array para um conjunto no sentido matemático é que um array – diferente de um conjunto - pode conter inúmeras unidades observacionais ou experimentas de mesmo valor. Nesses termos, um array possui estrutura homogênea e composta justamente por conter v.a. de mesmo tipo e por ser capaz de armazenas inúmeras realizações de um mesmo tipo de dado. Os arrays, a depender de sua estrutura são considerados unidimensionais e bidimensionais. Os arrays unidimensionais possuem um único índice para identificar cada elemento pertencente a ele. Imagine uma tabela de uma única linha; assim é estrutura um array unidimensional. Cada elemento está localizado em uma posição unidirecional, onde o primeiro valor pode possuir índice 1, o segundo elemento índice 2, o terceiro elemento índice 3 e assim sucessivamente. Tal índice funciona como um ponteiro que nos ajuda a percorrer a fila de v.a. contidas no array unidimensional. Os pontos de uma array unidimensional podem índices diferentes de uma ordem sequencial, desde que cada elemento do array possua um índice exclusivo dentro do conjunto que faz parte. Os arrays bidimensionais, também denominados matrizes, são estruturas onde cada v.a. contida no mesmo pode ser identificada por meio de dois índices, sendo que o primeiro índice se refere à posição vertical e o segundo índice se refere à posição horizontal. Tal descrição permite demonstrar que os arrays bidimensionais assumem forma de tabelas, onde as posições vertical e horizontal correspondem respectivamente às linhas e colunas de uma tabela. A compreensão de vetores e matrizes, ou arrays unidimensionais e arrays bidimensionais é importante, justamente para esclarecer questões sobre coleta e operacionalização de dados. Muitas vezes trabalhamos com tabelas, que nada mais são do que matrizes, que originalmente são coletadas e armazenadas em formatos distintos ao de uma tabela. Muitas vezes os dados de uma tabela podem estar contidos em uma array unidimensional e precisam ser tratados de forma a serem processados ou exibidos em forma de tabela. Como exposto acima, os arrays podem conter infinitos valores, os quais muitos podem ocorrer diversas vezes. Portanto, uma das preocupações de qualquer pesquisa que utiliza arrays e tabelas é identificar a frequência de ocorrência de cada valor, justamente para compreender os valores mais frequentes, os maiores e menores valores, etc. Toda e qualquer pesquisa que utilize tanto dados numéricos como categóricos se ocupa de compreender o comportamento desses dados e suas realizações (acontecimentos). A compreensão das realizações permite identificar o padrão de distribuição dos dados e suas frequências. Para este propósito a depender do tipo de dado analisado existem muitas técnicas para resumir as informações e em algumas situações o uso de tabelas se apresenta como uma solução rápida e simples de ser implementada, que pode ser utilizada tanto para análise de dados quantitativos ou qualitativos (v.a. categóricas), e até mesmo a ocorrência de ambos de forma associada. Imagine uma tabela contendo 18 valores a serem organizados em uma estrutura determinada por uma matriz de ordem 6X3, ou seja, seis linhas (eixo Y) e três colunas (eixo X). Estes dados podem se referir a seis elementos de amostragem constituídos de três atributos. Como exemplo, imagine uma turma de alunos da qual foi obtida a amostra constituída de seis alunos e suas respectivas notas em matemática, português e ciências. Os dados poderiam ser assim armazenados N={8.7, 8.9, 6.9, 6.3, 9.0, 7.0, 8.0, 7.9, 6.8, 5.2, 6.1, 6.3, 9.0, 6.2, 8.1, 6.3, 8.7, 7.1}, estes dados devem ser organizados em uma estrutura de dimensões 6x3 ou uma matriz M com i linhas e j colunas, sendo representadas como Mij tais que i=6 e j=3 que resultam na seguinte matriz/tabela:

Figura 19: Gráfico Polígono de Frequências

O Script R - 1: Construção de Uma matriz com três colunas apresenta a criação de uma matriz no R, idêntica à apresentada no modelo acima.

notas = c(8.7, 8.9, 6.9, 6.3, 9.0, 7.0, 8.0, 7.9, 6.8, 5.2, 6.1, 6.3, 9.0, 6.2, 8.1, 6.3, 8.7, 7.1)
matrix(notas, ncol = 3, byrow = TRUE)

##      [,1] [,2] [,3]
## [1,]  8.7  8.9  6.9
## [2,]  6.3  9.0  7.0
## [3,]  8.0  7.9  6.8
## [4,]  5.2  6.1  6.3
## [5,]  9.0  6.2  8.1
## [6,]  6.3  8.7  7.1

Tal estrutura permite identificar em cada uma de suas caselas os componentes de uma matriz ‘M’ conforme identificados na figura Figura 19: Matriz de ordem 6x3. Note que pelos índices ij, a matriz é preenchida da esquerda para a direita e de cima para baixo. Um exemplo de matriz e seus índices pode ser obtido quando analisamos os índices de planilhas eletrônicas tais como a planilha Calc do LibreOffice ou a planilha Excel do Microsoft Office.

Figura 20: Matriz de ordem 6x3

Uma vez compreendido como são estruturas tabelas de dados e que medidas computacionais extras podem ser requeridas para operacionalizar a estruturação das mesmas, cabe identificar os usos mais comuns e recomendáveis desse tipo de apresentação de dados. Via de regra dados tabulares são organizados mantendo identificadores na primeira linha e primeira coluna, com o objetivo de identificar os atributos e índices das v.a.. A primeira linha de uma tabela costuma conter os nomes dos atributos ou variáveis de cada coluna, a primeira célula de cada linha apresenta o índice da observação de modo a identificar cada uma de modo único. Um modo corriqueiro de utilizar tabelas é quando se deseja armazenar listas de dados não associados com frequências ou resumos de dados, como demonstrado na Tabela 5: Tabela de Clientes, este tipo de tabela, trata na realidade de armazenamentos de dados em forma de listagem. Tal configuração de tabelas permite acessar dados, mas não os organiza de modo a gerar alguma informação. Para obter informações relevantes a partir deste tipo de tabela, seus dados precisam ser acessados e processados de modo a permitir a obtenção de novas tabelas de resumo, onde os dados possam ser dispostos em um formato claro e conciso, tornando os dados de fácil apreensão.

Tabela 5: Tabela de Clientes

O exemplo de tabela acima é largamente utilizado, embora não seja uma forma clara e intuitiva. A granularidade da tabela não permite identificar padrões entre os clientes, justamente por não haverem classes ou intervalos de grupamento relacionados que permitam identificar correspondências entre as diferentes observações. No entanto tratamentos podem ser aplicados a tais conjuntos de dados, de forma a estabelecer classes úteis para compreensão do comportamento das v.a. que constituem o conjunto observacional. Se esta tabela contiver registros de 874 empresas, como ter ideia das relações presentes nela, quais padrões podem ser identificados? Tabelas extensas dificultam a identificação do comportamento das medidas de interesse, mas ao mesmo tempo o número de dados que armazenamos crescem exponencialmente, o que torna enfadonho o trabalho de análise e compreensão de tabelas extensas com informações granulares. Tais tabelas fornecem gotas de informação em um volume tão grande que impede a compreensão do comportamento dos mesmos. Uma alternativa para uma correta compreensão dos dados e identificação do comportamento dos atributos das v.a. de cada conjunto é estabelecer tabelas de caracterização que forneçam medidas de resumo como na Tabela 6: Tíquete e desconto médio por classe de empresa, que permitam realizar inferências sobre a população de empresas que constituem a clientela no cenário proposto.

Tabela 6: Tíquete e desconto médio por classe de empresa

Muitas vezes as medidas de resumo como as médias apresentadas são insuficientes para identificar características explicativas de um domínio de interesse. Uma alternativa pode ser recorrer a tabelas de frequências de ocorrência como na tabela 7. Note que a classe das empresas é uma v.a. qualitativa por natureza, e, portanto, não numérica; no entanto é possível atribuir valores numéricos a cada uma das classes relacionadas às empresas, um modo de realizar essa transformação é a atribuição da frequência de ocorrências de cada classe; assim se houverem 18 empresas da classe “A”, a classe A receberá como valor do seu atributo o valor 18. Embora seja um avanço na descrição dos dados, o valor da frequência absoluta nos diz algo, mas não nos diz tudo. Para obter uma informação mais acurada e representativa, a solução é utilizar a frequência relativa, que representa a proporção ou percentual dessa classe em relação ao todo. Para fins estatísticos entende-se como classe toda categoria que assimile dados qualitativos; como frequência de classe entende-se o número de realizações ou observações dos dados que corresponde a cada classe e a frequência relativa de classe como o resultado da divisão de cada frequência de classe pelo total de observações.

Tabela 7: Número de Empresas por Classe

O uso de tabelas, como exemplificado acima, informa muito mais do que tabelas de listagem como no caso da Tabela 5: Tabela de Clientes; mas não contribui significativamente para compreender características peculiares e relações entre diferentes informações. Para este fim uma boa solução são as tabelas de dupla entrada, que associam dois atributos de modo a identificar a frequência relativa de um atributo em relação ao outro. Tal medida nos dá a distribuição das v.a. de acordo com as associações possíveis dos pares ordenados de dados, ainda considerando o exemplo da empresa acima os dados poderiam ser arranjados em uma tabela de dupla entrada como exibido na Tabela 8: Dupla entrada de dados.

Tabela 8: Dupla entrada de dados

Note o maior grau de detalhamento e composição dos dados. Este arranjo permite identificar as frequências relativas, e claro, os pares ordenados com frequências mais comuns, pares com as maiores e menores frequências relativas. Além de criar subconjuntos de dados de acordo com as classes em que as empresas estão inscritas, o uso da Tabela 8: Dupla entrada de dados, utilizou um artifício muito interessante ao classificar a variável ‘tíquete médio’ que possui uma granularidade significativa e que por ser uma v.a. contínua dificulta sua enumeração. Para este caso a solução adotada foi utilizar dados intervalares ou dados agrupados, nos quais podem ser atribuídos os valores de tíquete médio de cada empresa; assim, uma empresa com tíquete médio de 6452.21 será atribuída à terceira classe [5000 - 9999] que compõe o intervalo compreendido pelos valores R$ 5000,00 e R$ 9999,00. Note que para este exemplo os intervalos de dados possuem amplitudes diferenciadas, na maioria dos casos, os intervalos possuem a mesma amplitude; porém, em casos específicos, os intervalos podem ser definidos de acordo com o cenário do mundo real de onde as v.a. provem onde são mensuradas em intervalos prescritos. Dados intervalares são conjuntos de dados atribuídos a um range ou intervalo pré-estabelecido que facilita a enumeração de realizações, uma vez que dados similares ou próximos podem ser reunidos em uma pseudo-classe, que passa a ser o elemento aglutinador dos dados, viabilizando o uso de tabelas para v.a. contínuas. Este tipo de organização dos dados resume as propriedades mais importantes das distribuições. A definição de intervalos de dados pode ser definida por meio de técnicas matemáticas ou de acordo com a conveniência de quem organiza os dados, caso este conheça um intervalo que reproduza algum intervalo de dados coerente com sua prática cotidiana da v.a. em questão. Um exemplo de usos de intervalos específicos pode ser verificado no artigo “Soroprevalência da infecção por Helicobacter pylori em uma amostra rural do Estado do Amazonas, Brasil”, publicado na Revista Pan-Amazônica de Saúde em 2012. Os dados da pesquisa foram apresentados na Tabela 9: Frequência da presença de anticorpos IgG contra H.pylori em duas faixas etárias; este exemplo utiliza dois intervalos referentes às faixas etárias de interesse para o estudo; embora o artigo não indique isso como hipótese de estudo, os dados permitem identificar nessa amostra uma prevalência da doença na faixa etária de crianças e adolescentes pertencentes à população que deu origem à amostra. Em estudos epidemiológicos como este, a identificação de faixas etárias especificas é bastante comum, o que leva ao uso de intervalos pré-definidos que dialogam com a literatura médica especializada, de modo a manter a comunicação e tornar os estudos replicáveis e comparáveis.

Tabela 9: Frequência da presença de anticorpos IgG contra H.pylori em duas faixas etárias

O exemplo da Tabela 8: Dupla entrada de dados, consiste em uma coleção de observações das v.a. tíquete médio e classe em cada par ordenado; visando justamente detalhar a ocorrência de cada par ordenado. Para este tipo de tabela para cada K elementos haverá n1 possíveis classes de tíquete médio e n2 possíveis classes de categoria de empresa. A combinatória de valores n1 e n2 resulta no número de possíveis pares ordenados que correspondem ao produto de n1 e n2. Dizendo de outra forma para cada n1 haverá n2 possibilidades de pares correspondentes. Como será visto a frente as tabelas de dupla entrada são uteis para obtenção de proporções, probabilidades, valores e probabilidades marginais, variância, desvio padrão, esperança, etc.

Graus de Liberdade

A discussão sobre graus de liberdade parece gerar um certo constrangimento. Todos livros de estatística obrigatoriamente passam pela questão dos graus de liberdade, no entanto a maioria toma esse conceito e sua explicação como um assunto exotérico. Muitos livros estatísticos ao falarem de graus de liberdade se atém em explicar que quando calculamos certas estatísticas como variância, desvio padrão e ANOVA o uso de graus de liberdade é necessário sem desenvolver melhor esta discussão. Via de regra o primeiro contato que se tem com o conceito de graus de liberdade em estatística é quando é apresentado o cálculo da variância amostral dada pela fórmula ( 3 ), onde se obtém a soma do quadrado das diferenças e a divide pelo número de observações menos um grau de liberdade (n-1). A partir deste ponto a explicação é de que utilizar (n-1) gera um estimador mais próximo da verdadeira variância populacional. Ora, essa explicação é descrita de uma maneira tão simplista que parece dizer que em algum momento se testou a divisão da soma dos quadrados das diferenças por {….(n-3), (n-2) , (n-1) , (n-0) , (n+1) , (n+2) , (n+3)….} e se concluiu que n-1 seria o melhor estimador. A história contada dessa forma nào é a mais adequada. A explicação do uso de graus de liberdade é um tanto complexa e a intenção não é criar uma definição acabada do tema aqui, mas buscar clarear o mesmo, uma vez que a definição de graus de liberdade é um tema que inquieta até mesmo o autor deste texto. A definição acadêmica do conceito passa por discussões pertencentes álgebra linear, geometria de projeções de vetores e matrizes e chega no conceito estatístico de número de determinações amostrais independentes de uma amostra. Falar do número de determinações independentes significa dizer que a medida que utilizamos os dados amostrais para uma dada estimativa e a partir desta mesma estimativa realizamos uma nova estimativa, a segunda estimativa utiliza os dados amostrais com menos um grau de liberdade. Significa dizer que se for realizada uma amostragem S={x1, x2, x3, x4} e obter-se a média do conjunto por meio de (∑(x1,x2,x3,x4))/4 = 15, significa dizer que três dos quatros elementos amostrais são livres para variar, justamente porque o último valor não possui liberdade; pois ele deverá ser ajustado prescritivamente de modo que após obtida a soma das outras três observações o quarto elemento realize o valor tal que quando acrescido às outras três observações a divisão do conjunto por quatro obtenha como quociente o valor 15 e resto zero. Significa dizer que das quatro observações, após obtida a média, apenas três podem ser consumidas para estimar valores desconhecidos, ou seja apenas três observações dispõem de liberdade ou são independentes, restando à ultima constituir-se como complemento do conjunto para obter o valor médio especificado. Por isso o tamanho amostral é um elemento bastante discutido, pois a medida que o tamanho da amostra aumenta, o conjunto amostral dispõe de mais graus de liberdade, e, portanto, adquire maior capacidade de identificação na variabilidade dos dados. O exemplo acima, permite demonstrar que o número de graus de liberdade refere-se ao número de observações livres para variar, dada uma restrição imposta, nesse caso o valor da média (WITTE; WITTE, 2010). Quando calcula-se o valor da media não há restrição alguma, pois são somados os valores das observações e são divididos pelo número de elementos, no entanto quando são realizados cálculos como a variância há uma restrição, pois como é possível ver na formula ( 3 ) a soma dos quadrados das diferenças recorre ao valor da media, portanto, o valor da media já é fixo, então o denominador da variância amostral passa a ser (n-1) justamente porque n-1 elementos podem variar desde que o último elemento realize o valor que satisfaça o cálculo para a media utilizada no cálculo do numerador ∑(x ̅-x)^2. Se um conjunto amostral sobre horas medias de trabalho por semana de um trabalhador qualquer corresponde a 40 a uma amostragem de três semanas corresponde as seguintes valores S={36, 44, 42} a média desses valores será 40.66, as horas trabalhadas na quarta semana para adequar o conjunto à media prescrita será 38: (∑36,34,42,38)/4=40. Essa regra pode ser comprovada pelas três listas com media 10: S1{8, 10, 12} S2{7, 10, 13} e S3{6, 9, 15}; uma vez que os dois valores de cada lista sejam fixados o terceiro não possui liberdade para variar, antes ele deve corresponder ao valor que realize a media 10. Assim, os graus de liberdade correspondem as informações amostrais livres para variar e estimar o parâmetro alvo (MCCLAVE; SINCICH, 2013).

Como exposto, ao obtermos a média, a mesma é obtida diretamente de parâmetros concretos, constituintes da amostra que são o número de elementos amostrais e seus valores realizados, portanto com os graus de liberdade iguais a (n) ou número de elementos amostrais. Quando obtemos a média, sendo ela mesma uma variável aleatória, sacrificamos um grau de liberdade e, portanto, ao utilizarmos esta estimativa para outros cálculos os mesmos devem ser calculados considerando menos um grau de liberdade, portanto (n-1). Assim quando é realizado o cálculo de ANOVA, como será visto a frente, utilizamos menos dois graus de liberdade. Pois o cálculo de anova é realizado a partir de duas variâncias, como cada uma das variâncias para ser calculada utiliza a média, o uso de duas variâncias implica em menos dois graus de liberdade.

Medidas de Resumo de Dados

O uso de tabelas e gráficos é significativamente útil, mas não são os únicos meios de apresentação de informações sobre as observações; além desses recursos, outras informações adicionais podem ser obtidas para descreverem características importantes do conjunto amostral como um todo; tais medidas são denominadas medidas de resumo. Existem diversas medidas de resumo, as mais comumente utilizadas são a média, a moda, a mediana, a variância, o desvio padrão, associação, correlação, etc. Dito isso, é importante demonstrar que o uso de tabelas e gráficos deve seguir a compreensão dos cenários onde são aplicados e as informações relevantes que não são obtidas por meio de tabelas. Se um investidor visualiza a estatística descritiva das vendas de seus ativos na última semana por meio de tabelas e gráficos; ele pode ser surpreendido por péssimos resultados. Um investidor inexperiente e sem conhecimento estatístico de medidas de resumo básicas pode perder o sono com estes resultados; mas um investidor mais experiente pode tomar os resultados das mesmas operações nos últimos 20 anos e perceber que a média das liquidações dos ativos a longo prazo são superiores a este resultado desfavorável a curto prazo, esta conclusão é obtida de forma mais acurada quando se utilizam medidas de resumo e localização.

Medidas de Localização

Medidas de Centralidade | Achando o seu centro

Os recursos gráficos e tabulares são significativamente mais úteis que as tabelas de listagens; no entanto, estes resumos não explicam todas as características de uma v.a.. Outras medidas para explicar a distribuição e comportamento das v.a. são as medidas de localização.
Imagine uma amostra composta de valores x1, x2, x3,…….xn, um conjunto de dados como este possui uma infinidade de características que trazem informações relevantes sobre o conjunto amostral. Para identificar características que sejam representativas do conjunto amostral como um todo, as medidas de localização são excelentes maneiras de descrever o conjunto de dados. As medidas de localização podem ser divididas em medidas de tendência central, medidas de localização e medidas de dispersão. Como medidas de tendência central podemos identificar a média, moda e mediana, já como medidas de dispersão temos as mais conhecidas como variância e desvio padrão; há outras medidas de dispersão mais criteriosas como percentis, intervalos interquartílicos, desvio médio, assimetria e curtose.

Moda

A moda é o valor que representa a maior frequência de realizações nos dados. Exemplos de moda podem ser obtidos nos casos em que se realiza a enumeração dos valores de um conjunto amostral. O exemplo das idades de alunos do terceiro ano ajuda a ilustrar a obtenção da moda, que nesse caso será a idade com maior número de ocorrências; outro exemplo de moda pode ser o número de modelos de veículos vendidos em um determinado ano, o modelo que possuir o maior número de vendas representa a moda. Além desses exemplos podemos ir além e considerar uma pesquisa com jovens onde se deseja saber qual o sabor de refrigerante preferido conforme a Tabela 10: Pesquisa de preferência do sabor de refrigerantes, os dados da tabela permitem afirmar que a moda nesse caso é 33, apresentado graficamente na Figura 21.

Tabela 10: Pesquisa de preferência do sabor de refrigerantes

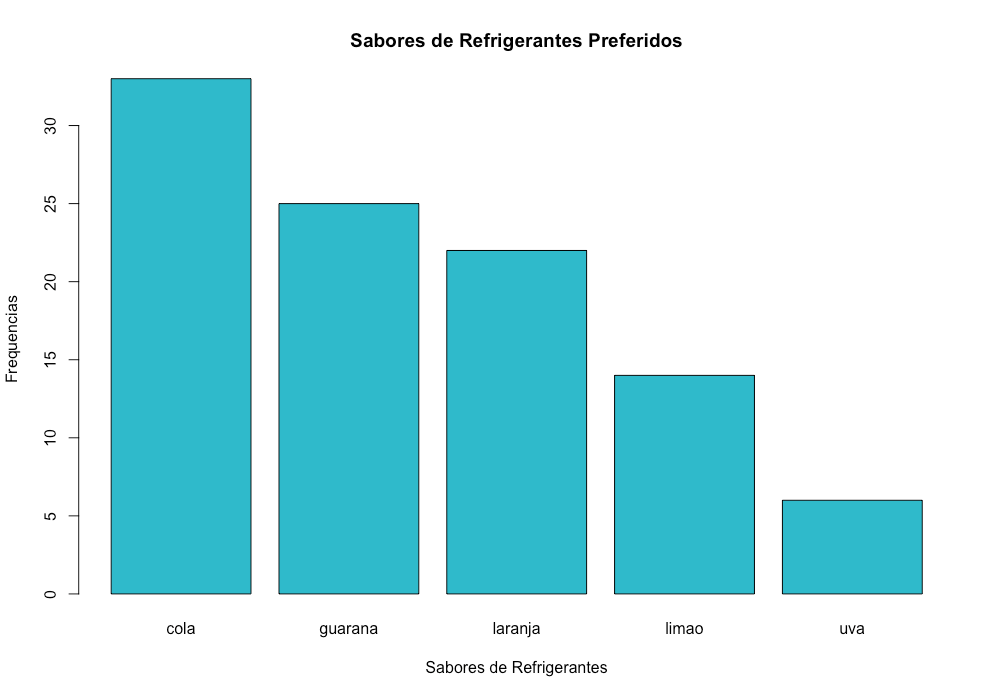
Figura 21: Grafico de preferências

Note que a moda representa o valor mais frequente do conjunto de dados. Outra forma simples de ilustrar a moda é tomando o seguinte conjunto amostral, representado pelas notas recebidas por um hambúrguer em um festival de degustação:

Notas = {8, 7, 9, 6, 7, 9, 4, 6, 4, 8, 9, 4, 8, 7, 8, 6, 7, 9, 6, 9, 6, 9, 4, 2}  

A nota 9 ocorre sete vezes, superando a frequência individuais de todas as outras notas. É justamente a realização da maior frequência em relação às demais notas que torna esta realização da v.a. em moda. Caso considerássemos essa amostra como um conjunto bimodal, teríamos as modas 9 e 6 apresentando respectivamente as frequências de ocorrência iguais a n9=7 e n6= 5. Estas demonstrações permitem concluir que a moda é a medida que permite concluir pela região em que uma v.a. se concentra. O Script R - 1 apresenta o código em R para criar a listagem de dados, a obtenção do número de unidades observacionais e por fim o código que retorna a moda do conjunto.

notas = c(8, 7, 9, 6, 7, 9, 4, 6, 4, 8, 9, 4, 8, 7, 8, 6, 7, 9, 6, 9, 6, 9, 4, 2)
length(notas)

## [1] 24

names(table(notas))[table(notas) == max(table(notas))]

## [1] "9"

A Figura 22: Moda de pesos de um time de futebol, mostra a moda dos pesos observados em um time de futebol constituído por onze jogadores. Esta figura demonstra esquematicamente que a moda é a frequência de valores que se destaca das demais.

Figura 22: Moda de pesos de um time de futebol

Por se tratar de frequências de ocorrências, a moda pode ser utilizada tanto para v.a. nominais como numéricas. Imagine que um fabricante de camisetas estampadas deseja saber as quatro cores de camisetas mais vendidas dentre o conjunto de oito cores disponíveis, para saber que tipo de equipamento e matéria prima utilizar na serigrafia. Nesse caso o espaço amostral seria constituído pelo seguinte conjunto Sn = {Branca, Preta, Azul, Amarela, Vermelha, Verde, Laranja, Cinza}. Se o conjunto em questão resultasse nas seguintes frequências Scn = (25, 11, 18, 8, 19, 9, 4, 21), estes dados permitem concluir que as modas identificadas são 25, 21, 19 e 18 para as cores branca, cinza, vermelha e azul respectivamente como apresentado na Figura 23: Frequências de cores mais vendidas.

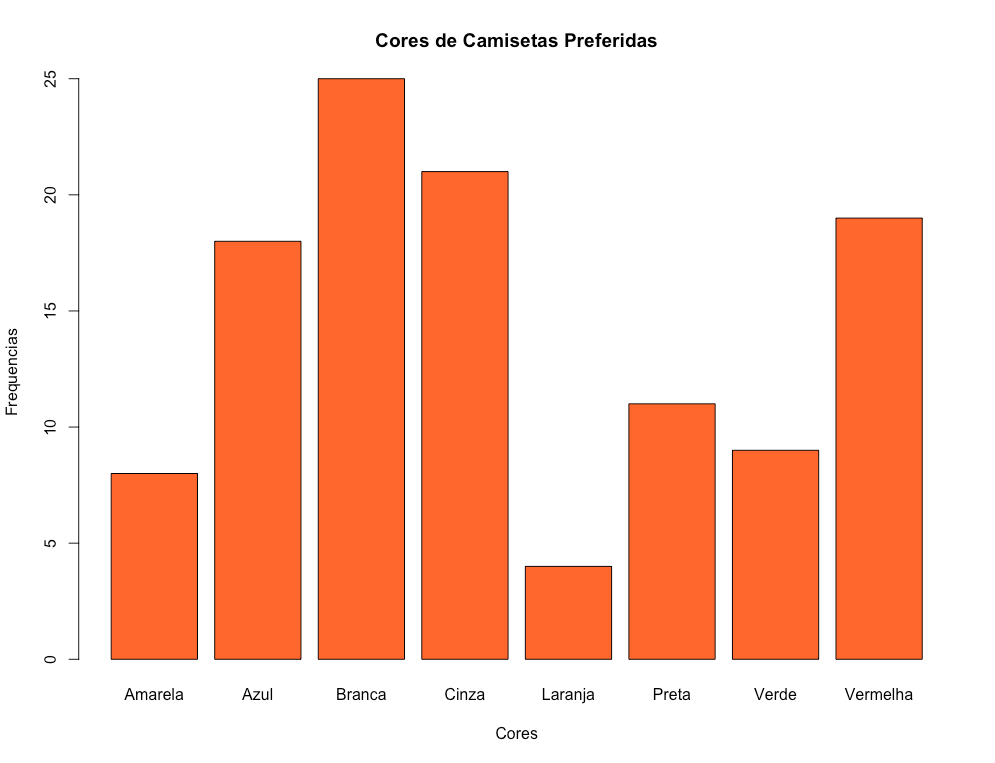
Frequências de cores mais vendidas

Média Aritmética

Médias são números nos quais os valores das v.a. estão centrados. A média é a medida de resumo mais conhecida, ela é obtida a partir da soma dos valores de todas as observações e a posterior divisão desse resultado pelo número de observações. Para conjuntos amostrais costumamos chamar a média aritmética da v.a. de media amostral, para conjuntos populacionais o conceito atribuído é de media populacional.

O Script R - 3 demonstra como obter a média das notas de forma direta por meio da função mean e também por meio mais prolixo obtendo a soma dos valores, o número de ocorrências e a posterior divisão da soma pelo número de ocorrências.

valores = c(8,7,9,6,7,9,4,6,4,8,9,4,8,7,8,6,7,9,6,9,6,9,4,2)
valores

##  [1] 8 7 9 6 7 9 4 6 4 8 9 4 8 7 8 6 7 9 6 9 6 9 4 2

mean(valores)

## [1] 6.75

sum(notas)

## [1] 162

length(notas)

## [1] 24

sum(notas)/length(notas)

## [1] 6.75

É importante apontar que muitas vezes a média é um valor que não pode ser realizado empiricamente, mas representa apenas uma medida de aproximação. No exemplo das notas obtidas, as notas resultam em números inteiros, enquanto que a média resulta em 6,75. A média representa o valor que corresponde ao valor de equilíbrio entre os valores. Para exemplificar o ponto de equilíbrio, imagine a média do peso de uma equipe de futebol.

Pesos = {86, 65, 70, 75, 60, 75, 95, 73, 79, 84, 80}

A média da equipe de jogadores representa o valor em torno do qual todos os valores realizados estão ao redor, esquematicamente a Figura 21: Comportamento da Média, simula todos os jogadores colocados em uma reta dispostos em sua ordem de grandeza de massa, os jogadores podem ser equilibrados sobre a reta quando o ponto de apoio representar o centro das distribuições de massa, este centro representa o centro da amostra, que constitui a média.

pesos = sample(60:100, 11, replace=T)
pesos

##  [1] 68 77 78 74 96 78 84 94 74 95 67

mean(pesos)

## [1] 80.45455

sort(pesos)

##  [1] 67 68 74 74 77 78 78 84 94 95 96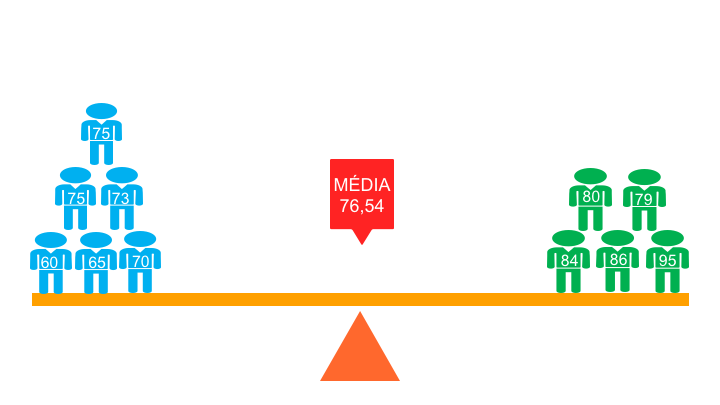

Figura 24: Comportamento da Média

Mediana

A mediana é obtida quando todos os dados de um conjunto amostral são organizados em ordem crescente da v.a., e então identifica-se a v.a. a qual mantem 50% das realizações abaixo dela, ou a antecedendo. Dito de outra forma, quando ordenamos os dados em ordem crescente a mediana é a v.a. que se situa ao centro do conjunto amostral. Recorrendo ao exemplo das notas: Notas = {8, 7, 9, 6, 7, 9, 4, 6, 4, 8, 9, 4, 8, 7, 8, 6, 7, 9, 6, 9, 6, 9, 4, 2}, se as ordenarmos como no exemplo abaixo, veremos que o conjunto amostral possui 24 valores, em casos como o ilustrado abaixo, a mediana é obtida realizando a média dos dois valores centrais que correspondem às posições 12 e 13, como as posições 12 e 13 correspondem ao valor 7 basta soma-las e dividir por dois resultando, é claro, no valor 7. Assim a mediana corresponde ao valor 7. Em casos onde o conjunto amostral possui um número ímpar de observações basta recuperar o valor central. Por exemplo se o conjunto fosse constituído de 25 unidades observacionais o item na 13º posição representaria a mediana

Notas = {2, 4, 4, 4, 4, 6, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9}

sort(notas)

##  [1] 2 4 4 4 4 6 6 6 6 6 7 7 7 7 8 8 8 8 9 9 9 9 9 9

median(notas)

## [1] 7

Figura 225: Localização da Mediana

Medidas de Dispersão | Saindo do Centro

Amplitude

A maneira mais breve e simples de se obter uma medida de dispersão é por meio da amplitude dos valores das observações, isso é feito subtraindo o menor valores realizado do maior valor realizado (DEVORE, [s.d.]). amplitude= max(obs)-mina(obs) Para a amostra de pesos do time de futebol a amplitude é obtida por meio do calculo amplitide=95-60=35. Quando realizamos diversas amostras em diferentes locais ou em diferentes momentos é possível comparar as amplitudes de cada amostragem para verificar se as amplitudes são semelhantes ou há alguma variabilidade nos dados: time_um=(55,65,69,70,74,78,85,85,87,88,90) time_dois=(60,70,71,72,73,74,75,76,77,78,95) Os exemplos dos times um e dois mostram diferentes realizações nos valores da v.a. peso, porém, com média e amplitude iguais para ambos os times como pode ser visto do código do Script R - 6: Obtenção de médias e amplitude dos times de futebol.

time_um = c(55,65,69,70,74,78,85,80,86,80,90)
time_dois = c(60,72,73,74,73,75,76,77,78,79,95)
mean(time_um)

## [1] 75.63636

mean(time_dois)

## [1] 75.63636

diff(range(time_um))

## [1] 35

diff(range(time_dois))

## [1] 35

Variância

variância também chamada a soma dos quadrados das diferenças é a primeira medida de variabilidade que se obtém de um conjunto amostral. A variância consiste em uma medida de variabilidade do conjunto de valores ao redor da média. Para obter a variância o procedimento consiste em obter a diferença entre os valores observados e a media, após a diferença de cada ocorrência é elevada ao quadrado, todos os quadrados obtidos são somados e divididos pelo tamanho da amostra; a elevação ao quadrado ocorre porque quando medimos a distância entre valores observados e a média encontramos tanto valores positivos como negativos que somados podem se anular e a elevação ao quadrado torna todos valores positivos evitando esse risco, no entanto essa medida apresenta uma medida de dispersão que difere em escala dos valores observados (DOWNING; CLARK, 2002). Quando calculamos a variância das duas populações do nosso exemplo a variância dos brasileiros é de 106.5 e a dos pigmeus de 93.3, note que estes valores fogem bastante dos valores médios e da variabilidade empírica observada. Isso torna a variância difícil de ser interpretado ou visualizada, por este motivo recorremos a um fator de correção, o desvio padrão. Variância => σ2 = E(X - µ) / N

Observe que as medidas de resumo da média e amplitude, são as mesmas para ambos os times do exemplo acima; no entanto não é possível estabelecer uma relação entre estes valores. Medidas de dispersão são uteis quando não apenas quando comparam dois conjuntos amostrais, mas também para descrever o conjunto individualmente. Para isso a variância deve ser mensurada a partir de um ponto ou valor de referência. A amplitude nos informa a distância entre o menor e o maior valor, mas até que ponto essa distância é grande ou pequena é difícil precisar, justamente porque não há um ponto de referência, ou uma escala para tanto. No caso da variância, a média é o valor de referência. A variância nos informa os desvios, ou distância das observações em relação à média. A variância deriva do cálculo do desvio médio absoluto. O desvio médio absoluto é obtido de acordo com a fórmula ( 1 ), onde obtemos a soma das diferenças das observações em relação à média e dividimos pelo número de observações (n):

    (∑|(x ̅-x)|)/n   (1)
    

A justificativa para utilizar o valor absoluto ou módulo das diferenças é que as diferenças negativas e positivas em relação à média se anulam, fazendo a variância tender a zero. As diferenças quando computadas em módulo retornam o valor absoluto de todas as diferenças |x ̅-x|. Feito isso é realizada a soma dos valores obtidos e a divisão da mesma pelo número de observações (DEVORE, [s.d.]). Em função de uma série de razões teóricas o cálculo da variância difere do cálculo do desvio médio absoluto tanto no numerador como no denominador a depender se a variância a ser calculada deriva de um conjunto populacional ou amostral. Enquanto o denominador do desvio médio absoluto é igual a (n), o denominador da variância populacional permanece como (n) demonstrado pela fórmula (2) e como (n-1) quando se tratar de variância amostral, demonstrado na fórmula ( 3 ). Já o numerador da variância tanto para amostras como populações corresponde ao quadrado das diferenças obtidas. Essa mudança resulta que a variância se relaciona em uma escala de expoente 2 em relação à escala original dos dados.

    (∑(x ̅-x)^2)/(n-1)   (2)

    (∑(x ̅-x)^2)/(n-1)   (3)
    

Embora a fórmula (3) nos apresente o cálculo para a obtenção da variância, a depender do tipo de dados constituintes do conjunto amostral, outras formulas de cálculo da variância são utilizados. Em momento oportuno quanto forem tratados os diferentes tipos de distribuições serão apresentadas as formulas de cálculo das variâncias das distribuições especificas.

Desvio Padrão

É sempre um desafio comparar valores distintos; por exemplo, como dizer se uma amostra está em uma escala comparável com os dados populacionais ou encontramos um novo padrão? Para comparar elementos diferentes ou amostras que possam conter novas informações precisamos recorrer a padrões que permitam aproximar informações e compará-las. As médias e desvios padrão são úteis neste processo. Precisamos de medidas padrão para comparar o que aparentemente não é comparável. O desvio padrão é obtido a partir da raiz quadrada da variância. Dessa forma o desvio padrão possui as mesmas unidades dos dados originais observados (GLANTZ, 2012). As raízes de σ2 das amostras consideradas são 10.3 para brasileiros e 9.6 para pigmeus. Considerando as medias de brasileiros 165.9 e pigmeus 64.5, se tomarmos o desvio padrão podemos identificar que o desvio padrão dos brasileiros encontra valores no intervalo entre 155.6 e 176.2 enquanto que entre os pigmeus esse intervalo localiza-se entre 54.9 e 74.2. O desvio padrão permite que tomemos amostras normalizadas onde atribuímos o valor zero à media e utilizamos os desvios padrão como unidade de medida de dispersão, para então fazer comparações. Assim comparamos o desvio padrão em relação à média de cada amostra. Desse modo é possível afirmar o quanto um desvio particular é diferente dos desvios de uma dada população. O desvio padrão pode ser calculado por meio das estatísticas T ou Z, via de regra quando a amostra possui um n > 30 utilizamos a estatística Z, muito embora quanto maior o n, mais uma estatística T se aproxime do padrão da curva normal da estatística Z, comportamentos que serão vistos mais adiante.

Coeficiente de Variação

Cv = S/x*100% ### Desvio Absoluto Mediano Pág 70 de (BUSSAB; MORETTIN, 2017)

Quantis

Os quantis são intervalos regulares de distribuições acumuladas, formando subconjuntos de dados. A obtenção dos quantis é realizada por meio dos percentis, que nada mais são do que o resultado da subdivisão do intervalo amostral em 100 partes – 100 quantis, independentemente do tamanho da amostra. Afim de facilitar a identificação dos mesmos de acordo com sua amplitude, podemos classificá-los como percentis 100-quantis, quintis 5-quantis, duo-deciles para dúzias, decis para dezenas, quartis para as quarta-partes da distribuição e os tercis para as terça-partes. Quando informamos que a avaliação de um aluno estava no 75º percentil, estamos informando que 75% dos demais alunos obtiveram nota menor que o aluno em questão. O uso de quantos pode ser aplicado tanto cara variáveis discretas como contínuas, em cada caso a obtenção dos quantis segue uma abordagem específica que será detalhada em momento oportuno.

Quantis Empíricos

…… (BUSSAB; MORETTIN, 2017) ### Intervalo-interquartílico …. ### Desvio Médio ….. ### Assimetria ou Curtose …

Distribuição Normal

As etapas preliminares nos apresentaram três importantes valores, o tamanho da população, a média e o desvio padrão. As amostras apresentam distribuição similar com 68% dos valores alocados a um desvio padrão da média e 95% a dois desvios padrão da media. Este padrão é bastante frequente, sobretudo para amostras grandes; tão frequente que constituiu um campo de pesquisa dos matemáticos. Onde suas conclusões apontam que este padrão é o resultado de fatores aleatórios independentes em que sua distribuição assume valores distribuídos uniformemente, tal que nas duas amostras consideradas, este fenômeno é chamado de distribuição normal ou gaussiana (GLANTZ, 2012). Esta distribuição é derivada inteiramente pela média populacional e seu desvio padrão.

Imagine uma população de 150 pigmeus com estaturas entre 50 e 80cm com média de 65cm com 95 % dos indivíduos possuindo altura entre 55 e 75cm e uma população de 250 brasileiros com alturas entre 150 e 180 cm, média de 165 e 95 da população com alturas entre 155 e 175. Embora existam diferenças entre as alturas médias, intervalos e variabilidade, as formas da distribuição são bastante semelhantes, resultando em distribuições normalizadas.

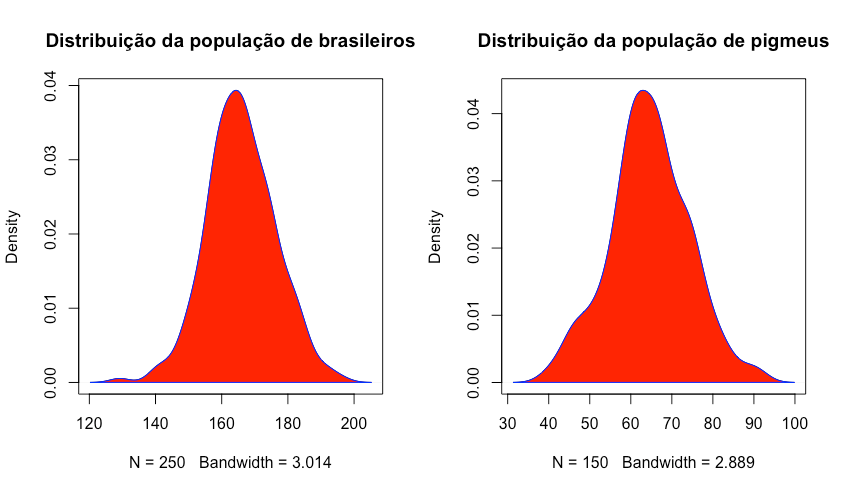
Figura 25: Distribuição Normal

As medias de brasileiros e pigmeus podem ser consideradas o intervalo de valores em que o menor e o maior valor definem a amplitude dos dados (DOWNING; CLARK, 2002; GLANTZ, 2012). No caso das medidas de altura estamos tratando de medidas intervalares discretas, uma vez que podem ser enumeradas e não são subdividas. Quando possuímos um conjunto amostral e obtemos estatísticas derivadas desse conjunto, costumamos obter o que chamamos de parâmetros da distribuição. E quando possuímos duas ou mais amostras semelhantes como no exemplo de brasileiros e pigmeus a análise se detém em descrever como elas diferem (DOWNING; CLARK, 2002).

Método da Máxima Verossimilhança

É um método para derivar estimadores. O método da máxima verossimilhança ou Likelihood é utilizado quando possuímos uma população com uma variável de interesse com distribuição conhecida e onde um ou mais parâmetros ‘θ’ são desconhecidos. Onde θ pode ser um valor real (para um parâmetro desconhecido) ou k parâmetros desconhecidos. Amostra Aleatória AA (x1, x2, xn) ~ IIDs, cujo objetivo é construir uma função da AA que permita obter inferências sobre θ. Esta função é então um estimador, ou seja uma função. Que depende da amostra aleatória mas é independente dos parâmetros desconhecidos. Um estimador bastante conhecido é o Método da Máxima Verossimilhança MMV. Logo, o MMV é uma função do parâmetro, ou dos parâmetros desconhecidos: Tal como: f(θ, x1, x2, xn), sendo que esta função assume diferentes propriedades para amostras continuas e discretas. No caso de amostras contínuas a função é a função densidade probabilidade conjunta dos valores de X: f f(θ, x1, x2, xn) => que é o produto das funções densidade probabilidade marginais, que é produto da função comum a todos elementos: Independes | Identicamente Distribuídas fx1(x1), fx2(x2), fxn(xn) = fx(x1), fx(x2), fx(xn)
Π fx(x)

Quando as variáveis são discretas nós temos então a função de probabilidade conjunta dos valores de X: f f(θ, x1, x2, xn); sem a densidade, devido a natureza da variável: Independes | Identicamente Distribuídas p(x1= x1), p(x2= x2), p(xn= xn) = p(x= x1), p(x= x2), p(x= xn) Π p(x=xi)

O estimador da máxima verossimilhança θ= θ(x1, x2,xn) é o estimador que vai maximizar para todos aos valores pertencentes ao espaço amostral a verossimilhança que determinamos. No caso de uma amostra particular teremos uma estimativa de máxima verossimilhança, que é a concretização do estimador para a amostra concreta. Esta estimativa é o argumento que maximiza para todos valores da amostra a função de verossimilhança. Para este fim realizamos a maximização da função de verossimilhança.

Ex1: x~Poisson(x), λ > 0? => amostra (x1, x2, xn) Precisamos determinar a função de verossimilhança: Π P(x=xi) = e- λ* λx / x!

Calcular o máximo dessa função é equivalente a calcular o máximo do seu logaritimo: Ln (λ ,x1, x2, xn) => calcular a derivada

A Estimatitiva da Maxima Verossimilhanca EMV = a media de X = X => EMV = λ.

Ex2: x~Exponencial (μ), μ? => amostra (x1, x2, xn) Precisamos determinar a função de verossimilhança: Π fx(xi) = e- λ* λx / x! Calcular o máximo dessa função é equivalente a calcular o máximo do seu logaritimo: Ln(μ, x1, x2, xn)

A Estimatitiva da Maxima Verossimilhanca EMV = n/ Σxi = 1/x = inverso da media amostral