3
Medidas de Centralidade
Achando seu centro
A média é a maneira mais óbvia, direta e prética de resumir dados. Basicamente a maioria das análises se utiliza da média para obtenção de resultados.
Vamos inicialmente criar uma lista de dados para extrair informações referentes à mesma:
library(ggplot2)
library(foreign)
acidentes = read.dbf("data/acidentes.dbf")
head(acidentes)## ID LONGITUDE LATITUDE LOG1 LOG2 PREDIAL1
## 1 660953 0 0 AV ASSIS BRASIL <NA> 6699
## 2 660956 0 0 R DR BARROS CASSAL <NA> 411
## 3 660959 0 0 AV FABIO ARAUJO SANTOS <NA> 1500
## 4 660962 0 0 AV IPIRANGA <NA> 8799
## 5 660963 0 0 AV ASSIS BRASIL <NA> 164
## 6 661175 0 0 AV IPIRANGA R SAO MANOEL 0
## LOCAL TIPO_ACID LOCAL_VIA QUEDA_ARR DATA
## 1 Logradouro ABALROAMENTO 6699 AV ASSIS BRASIL 0 2019-01-01
## 2 Logradouro ABALROAMENTO 411 R DR BARROS CASSAL 0 2019-01-01
## 3 Logradouro CHOQUE 1500 AV FABIO ARAUJO SANTOS 0 2019-01-01
## 4 Logradouro COLISAO 8799 AV IPIRANGA 0 2019-01-01
## 5 Logradouro ABALROAMENTO 164 AV ASSIS BRASIL 0 2019-01-01
## 6 Cruzamento ABALROAMENTO AV IPIRANGA & R SAO MANOEL 0 2019-01-01
## DIA_SEM HORA FERIDOS FERIDOS_GR MORTES MORTE_POST FATAIS AUTO TAXI
## 1 TERCA-FEIRA 02:45 1 0 0 0 0 3 0
## 2 TERCA-FEIRA 07:36 1 0 0 0 0 2 0
## 3 TERCA-FEIRA 16:50 4 0 0 0 0 1 0
## 4 TERCA-FEIRA 19:00 5 0 0 0 0 3 0
## 5 TERCA-FEIRA 22:15 1 0 0 0 0 1 0
## 6 TERCA-FEIRA 04:10 0 0 0 0 0 2 0
## LOTACAO ONIBUS_URB ONIBUS_MET ONIBUS_INT CAMINHAO MOTO CARROCA BICICLETA
## 1 0 0 0 0 0 0 0 0
## 2 0 0 0 0 0 0 0 0
## 3 0 0 0 0 0 0 0 0
## 4 0 0 0 0 0 0 0 0
## 5 0 0 0 0 0 1 0 0
## 6 0 0 0 0 0 0 0 0
## OUTRO TEMPO NOITE_DIA FONTE BOLETIM REGIAO DIA MES ANO FX_HORA CONT_ACID
## 1 0 BOM NOITE DEPTRAN 000219 NORTE 1 1 2019 2 1
## 2 0 BOM DIA DEPTRAN 000519 CENTRO 1 1 2019 7 1
## 3 0 BOM DIA DEPTRAN 000919 SUL 1 1 2019 16 1
## 4 0 BOM NOITE DEPTRAN 001119 LESTE 1 1 2019 19 1
## 5 0 BOM NOITE DEPTRAN 001219 NORTE 1 1 2019 22 1
## 6 0 BOM NOITE EPTC 230995 LESTE 1 1 2019 4 1
## CONT_VIT UPS CONSORCIO CORREDOR
## 1 1 5 <NA> 0
## 2 1 5 <NA> 0
## 3 1 5 <NA> 0
## 4 1 5 <NA> 0
## 5 1 5 <NA> 0
## 6 0 1 <NA> 0dim(acidentes)## [1] 7878 43A obtenção da média meículos envolvidos em acidentes pode ser obtido pela soma de veículos envolvidos, dividido pelo numero de ocorrências:
sum(acidentes$AUTO)/length(acidentes$AUTO)## [1] 1.462554Ou por meio da função mean():
mean(acidentes$AUTO)## [1] 1.462554Também podemos obter a média de um subconjunto de dados, tais como por exemplo acidentes em cruzamentos:
mean(acidentes[acidentes$LOCAL=="Cruzamento",]$AUTO)## [1] 1.676241O mesmo podendo ser feito para logradouros
mean(acidentes[acidentes$LOCAL=="Logradouro",]$AUTO)## [1] 1.387191Agora filtrando por abalroamento
mean(acidentes[acidentes$TIPO_ACID=="ABALROAMENTO",]$AUTO)## [1] 1.459652Agora filtrando por atropelamento, note que o valor é de menor um automóvel por atropelamento, por que existem atropelamento por outras categorias de veículos.
mean(acidentes[acidentes$TIPO_ACID=="ATROPELAMENTO",]$AUTO)## [1] 0.5665399Verificando se a media de automóveis envolvidos varia entre logradouro e cruzamento:
mean(acidentes[acidentes$TIPO_ACID=="ATROPELAMENTO" & acidentes$LOCAL =="Logradouro",]$AUTO)## [1] 0.5661479mean(acidentes[acidentes$TIPO_ACID=="ATROPELAMENTO" & acidentes$LOCAL =="Cruzamento",]$AUTO)## [1] 0.5833333library(MASS)
ggplot(Cars93, aes(x=Horsepower)) +
geom_histogram(color="black", fill="white",binwidth = 10)+
facet_wrap(~Origin)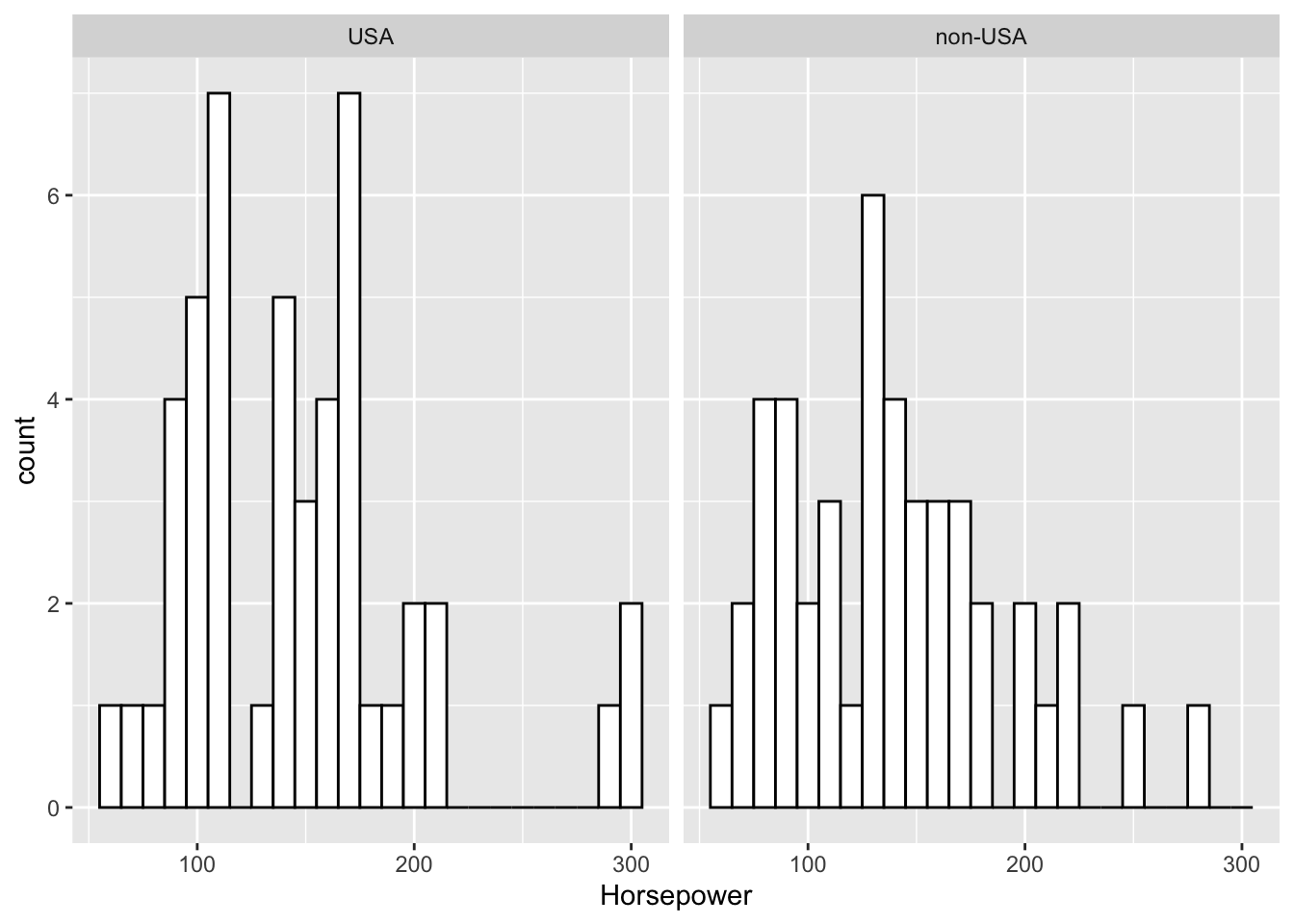
ggplot(acidentes[acidentes$FATAIS > 0, ], aes(x=FATAIS, )) +
geom_histogram(color="black", fill="white",binwidth = 10)+
facet_wrap(~LOCAL)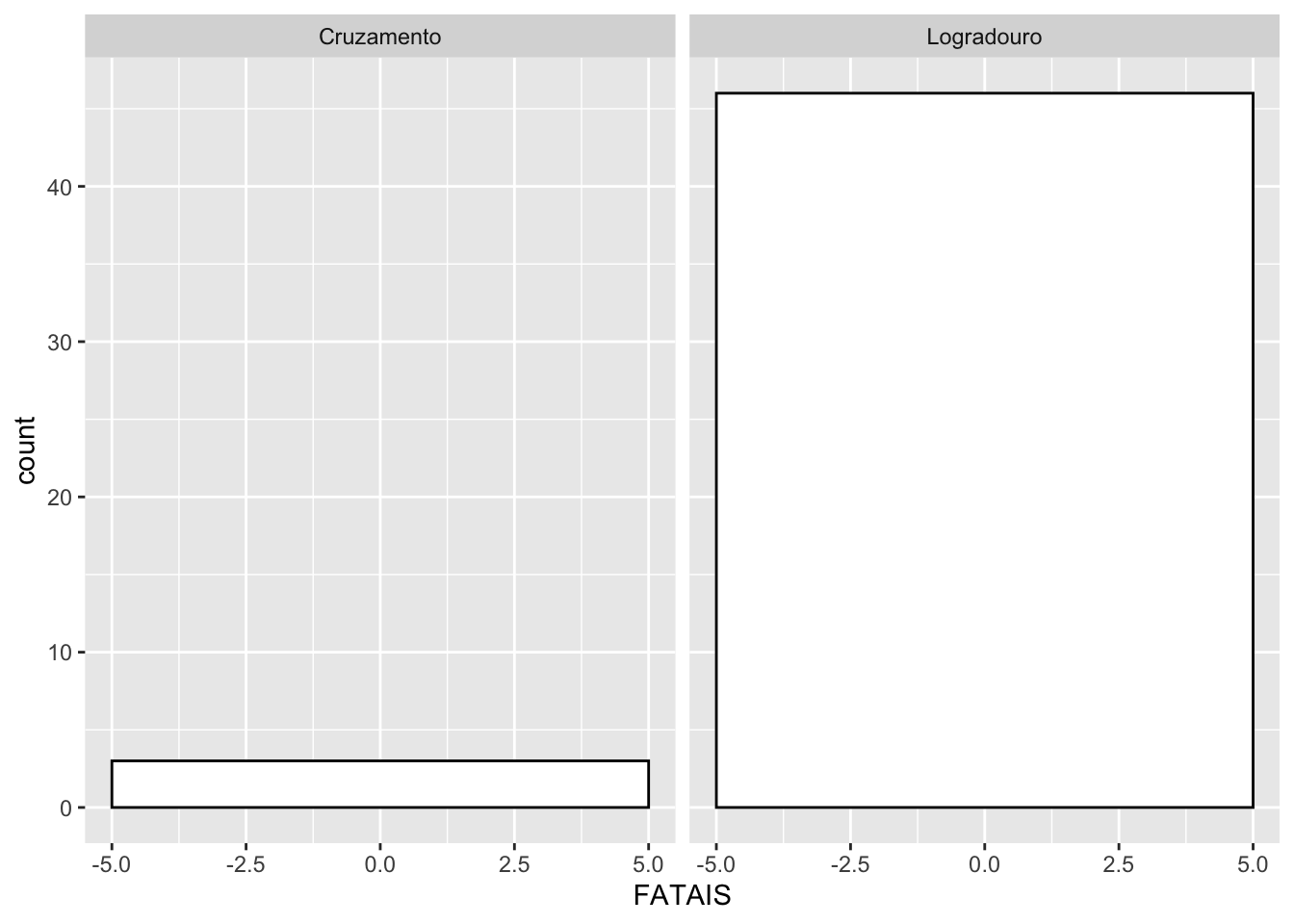
Aparando a média
Uma solução para discrepâncias de médias é utilizar a média aparada, uma solução utilizada é eliminar valores nas pontas. Uma aplicação bastante comum é eliminar dados acima de dois desvios padrão ou também obter a média dos 95%, eliminando 2,5% nas extremidades:
mean(Cars93$Horsepower)## [1] 143.828mean(Cars93$Horsepower, trim = 0.05)## [1] 140.4941mean(acidentes$AUTO)## [1] 1.462554mean(acidentes$AUTO, trim = 0.025)## [1] 1.451509Média geométrica
O R não fornece uma função direta para a média geométrica, mas conhecendo o fórmula da mesma é fácil de implementá-la:
dados = c(1.10, 1.15, 1.10, 1.20, 1.05)
res = prod(dados)^(1/length(dados))
res## [1] 1.118847Média Harmônica
Se demanhã você sai de carro para o trabalho e não tem a menor pressa de chegar, a média de velocidade de percurso é relativamente baixa, no entando ao final da tarde pode acontecer de você querer chegar o mais breve possível me casa. Qual a taxa média de seu tempo total de percurso?
velocidades = c(35, 60)
1/velocidades## [1] 0.02857143 0.01666667media_harmonica = 1/mean(1/velocidades)
media_harmonica## [1] 44.21053Mediana
Como a média é sensível a valores extremos, uma outra medida de centralidade por vezes útil é a mediana; a mediana nos retorna o valor central de todos os números, ou seja, se ordenarmos as unidades observacionais pelo seu valor, a mediana será a unidade ao centro, ou a média das duas medidas ao centro. Para este fim iremos analisar a mediana do número de veículos envolvidos em acidentes fatais, envolvendo a classe automóvel
autos = acidentes[acidentes$FATAIS > 0 & acidentes$AUTO > 0, ]$AUTO
median(autos)## [1] 1autos = acidentes[acidentes$FX_HORA > 0 & acidentes$AUTO > 0, ]$FX_HORA
autos = na.exclude(autos)
median(autos)## [1] 13moto = acidentes[acidentes$FX_HORA > 0 & acidentes$MOTO > 0, ]$FX_HORA
moto = na.exclude(moto)
median(moto)## [1] 15autos = acidentes[acidentes$FERIDOS > 0 & acidentes$MOTO > 0, ]$FERIDOS
autos = na.exclude(autos)
median(autos)## [1] 1Estatística à moda da casa
A moda é a medida de centralidade que nos aprasenta o valor que gera o vértice da nossa distribuição:
library(modeest)
#most frequente value
fx = acidentes$FX_HORA
fx = na.exclude(fx)
mfv(fx)## [1] 8Tal estatística fica demonstrada por meio da função table:
table(acidentes$FX_HORA)##
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## 110 86 44 34 52 73 179 432 570 490 506 518 536 551 527 567 535 409 499 365
## 20 21 22 23
## 265 212 191 122