3
Tipos de DistribuiçõesDistribuições
Utilizamos distribuições padrão pela dificuldade de cálculo e falta de meios computacionais para calcular a distribuição específica de um conjunto de dados.
Uma aproximação de distribuição permite identificar u bom ajusteo com pequeno erro percentual em relacão à distribuição original.
Distribuição Normal
As etapas preliminares nos apresentaram três importantes valores, o tamanho da população, a média e o desvio padrão. As amostras apresentam distribuição similar com 68% dos valores alocados a um desvio padrão da média e 95% a dois desvios padrão da media. Este padrão é bastante frequente, sobretudo para amostras grandes; tão frequente que constituiu um campo de pesquisa dos matemáticos. Onde suas conclusões apontam que este padrão é o resultado de fatores aleatórios independentes em que sua distribuição assume valores distribuídos uniformemente, tal que nas duas amostras consideradas, este fenômeno é chamado de distribuição normal ou gaussiana (GLANTZ, 2012). Esta distribuição é derivada inteiramente pela média populacional e seu desvio padrão.
Imagine uma população de 150 pigmeus com estaturas entre 50 e 80cm com média de 65cm com 95 % dos indivíduos possuindo altura entre 55 e 75cm e uma população de 250 brasileiros com alturas entre 150 e 180 cm, média de 165 e 95 da população com alturas entre 155 e 175. Embora existam diferenças entre as alturas médias, intervalos e variabilidade, as formas da distribuição são bastante semelhantes, resultando em distribuições normalizadas.
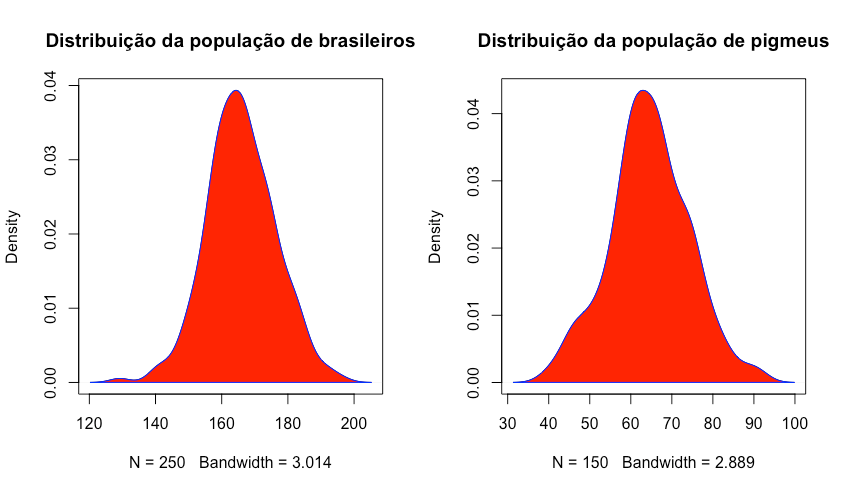
Figura 25: Distribuição Normal
As medias de brasileiros e pigmeus podem ser consideradas o intervalo de valores em que o menor e o maior valor definem a amplitude dos dados (DOWNING; CLARK, 2002; GLANTZ, 2012). No caso das medidas de altura estamos tratando de medidas intervalares discretas, uma vez que podem ser enumeradas e não são subdividas. Quando possuímos um conjunto amostral e obtemos estatísticas derivadas desse conjunto, costumamos obter o que chamamos de parâmetros da distribuição. E quando possuímos duas ou mais amostras semelhantes como no exemplo de brasileiros e pigmeus a análise se detém em descrever como elas diferem (DOWNING; CLARK, 2002).
Distribuição de Poisson
Distribuição Markoviana
Distribuição Exponencial
#Identificando uma distribução
## [1] 1.753291 1.919886 1.976526 1.952918 1.864170 2.006332 2.114065 2.017388
## [9] 1.807543 1.944525 1.895914 2.135433 1.954162 2.049140 1.957816 1.938236
## [17] 1.914842 1.990760 2.301209 2.044261 1.960871 2.086531 2.094910 2.080329
## [25] 1.893349 1.812500 2.086628 2.177451 2.089319 2.035600 1.996644 2.042127
## [33] 1.979418 2.034733 1.920986 1.974881 1.984626 2.003020 1.991984 2.042423
## [41] 2.056126 2.144029 1.861899 2.039602 1.916456 1.794874 1.899774 1.961376
## [49] 2.088906 1.992153 1.988307 2.098516 2.010027 2.118794 2.060574 1.913828
## [57] 2.029583 2.009447 2.057665 1.848029 2.046761 1.962463 1.963421 1.980486
## [65] 2.009477 2.052357 1.885009 2.051056 1.960344 1.953989 2.186500 1.748407
## [73] 1.705471 2.068965 1.921871 2.188815 2.082937 1.970224 1.810628 2.109574
## [81] 1.727361 1.932089 1.999241 1.885270 1.908680 1.780994 1.952034 1.971518
## [89] 2.091494 2.078309 2.029021 2.163567 2.076701 2.184105 1.932282 1.890947
## [97] 1.913305 1.957423 1.980485 1.966300 2.021707 1.886257 1.918351 2.217027
## [105] 1.932500 2.001083 2.028254 1.829714 2.010224 1.976427 2.055425 1.925367
## [113] 2.047060 2.052046 2.129452 2.202760 1.897251 2.150757 1.958918 2.033790
## [121] 1.925449 1.972894 2.057249 1.810718 1.928875 2.010506 2.084064 1.952038
## [129] 1.925980 1.984573 2.093603 1.916619 1.899385 2.064533 1.811898 1.935841
## [137] 1.902347 2.033480 1.912898 1.795360 2.112731 1.922188 2.035704 1.956176
## [145] 2.231342 2.152290 2.063216 2.000139 2.231623 2.064015## [1] 49.19349 57.82827 62.72547 58.12549 52.17689 58.55029 62.84157 60.68372
## [9] 56.47949 55.89055 56.47175 65.05970 59.71260 57.91736 58.75351 60.24343
## [17] 59.72172 56.59941 71.42080 60.69744 58.55539 63.60583 61.24562 61.34658
## [25] 58.39472 56.71224 61.32760 65.47646 65.94768 58.29633 57.45515 60.64784
## [33] 56.25822 62.59725 59.04130 59.04992 58.06056 61.49884 60.10287 57.87646
## [41] 58.99464 63.79971 56.02514 62.10444 56.35855 52.47614 56.74269 59.03610
## [49] 63.42570 58.65400 57.28594 60.11894 58.26592 64.61149 60.37932 56.53390
## [57] 62.83849 60.00384 64.32317 56.04324 59.96322 60.98848 55.89666 58.40639
## [65] 61.75169 62.52863 58.96361 61.81815 58.57125 58.47007 65.82906 52.39848
## [73] 50.70806 62.06120 60.04213 65.63758 64.50656 57.23154 56.54750 59.92107
## [81] 50.58532 58.06701 56.74736 59.09588 58.90381 51.49029 59.72501 54.28005
## [89] 65.47642 63.99687 60.68258 64.75503 64.60923 68.28830 55.62770 60.59066
## [97] 56.62911 60.00935 62.88552 60.84199 60.55956 60.12722 54.96506 66.92706
## [105] 59.25301 60.16743 61.56726 53.67556 58.83546 59.03888 59.77550 62.02406
## [113] 61.59138 61.65169 67.40009 68.44888 55.08326 65.20532 60.36351 63.50490
## [121] 57.44520 54.09604 58.82077 53.85267 57.95686 61.39594 64.23424 59.56509
## [129] 57.19908 58.93671 61.63141 57.10336 53.99828 61.80349 51.00167 57.98726
## [137] 60.38600 63.50032 54.90174 57.22104 60.79511 57.00789 61.38594 62.42284
## [145] 67.57155 63.66792 59.15684 61.69050 63.86392 62.59285
##
## Call:
## lm(formula = b ~ a)
##
## Coefficients:
## (Intercept) a
## -1.141 30.558plot(a, b, pch = 16, cex = 1.3, col = "blue", main = "Regressão Linear", xlab = "Altura (cm)", ylab = "Peso (kg)")
abline(lm(b ~ a))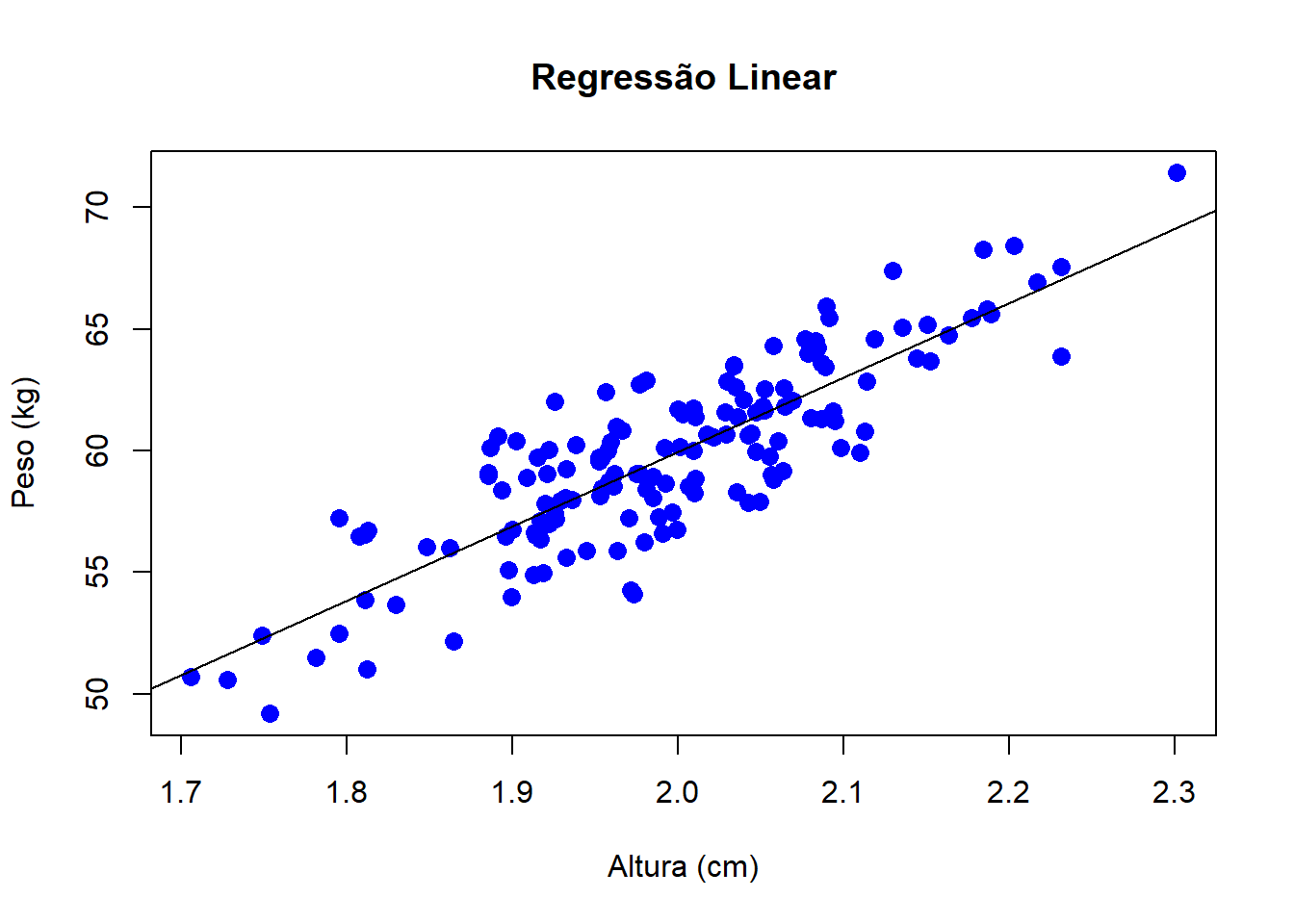
Método da Máxima Verossimilhança
É um método para derivar estimadores. O método da máxima verossimilhança ou Likelihood é utilizado quando possuímos uma população com uma variável de interesse com distribuição conhecida e onde um ou mais parâmetros ‘θ’ são desconhecidos. Onde θ pode ser um valor real (para um parâmetro desconhecido) ou k parâmetros desconhecidos. Amostra Aleatória AA (x1, x2, xn) ~ IIDs, cujo objetivo é construir uma função da AA que permita obter inferências sobre θ. Esta função é então um estimador, ou seja uma função. Que depende da amostra aleatória mas é independente dos parâmetros desconhecidos. Um estimador bastante conhecido é o Método da Máxima Verossimilhança MMV. Logo, o MMV é uma função do parâmetro, ou dos parâmetros desconhecidos: Tal como: f(θ, x1, x2, xn), sendo que esta função assume diferentes propriedades para amostras continuas e discretas. No caso de amostras contínuas a função é a função densidade probabilidade conjunta dos valores de X: f f(θ, x1, x2, xn) => que é o produto das funções densidade probabilidade marginais, que é produto da função comum a todos elementos: Independes | Identicamente Distribuídas fx1(x1), fx2(x2), fxn(xn) = fx(x1), fx(x2), fx(xn)
Π fx(x)
Quando as variáveis são discretas nós temos então a função de probabilidade conjunta dos valores de X: f f(θ, x1, x2, xn); sem a densidade, devido a natureza da variável: Independes | Identicamente Distribuídas p(x1= x1), p(x2= x2), p(xn= xn) = p(x= x1), p(x= x2), p(x= xn) Π p(x=xi)
O estimador da máxima verossimilhança θ= θ(x1, x2,xn) é o estimador que vai maximizar para todos aos valores pertencentes ao espaço amostral a verossimilhança que determinamos. No caso de uma amostra particular teremos uma estimativa de máxima verossimilhança, que é a concretização do estimador para a amostra concreta. Esta estimativa é o argumento que maximiza para todos valores da amostra a função de verossimilhança. Para este fim realizamos a maximização da função de verossimilhança.
Ex1: x~Poisson(x), λ > 0? => amostra (x1, x2, xn) Precisamos determinar a função de verossimilhança: Π P(x=xi) = e- λ* λx / x!
Calcular o máximo dessa função é equivalente a calcular o máximo do seu logaritimo: Ln (λ ,x1, x2, xn) => calcular a derivada
A Estimatitiva da Maxima Verossimilhanca EMV = a media de X = X => EMV = λ.
Ex2: x~Exponencial (μ), μ? => amostra (x1, x2, xn) Precisamos determinar a função de verossimilhança: Π fx(xi) = e- λ* λx / x! Calcular o máximo dessa função é equivalente a calcular o máximo do seu logaritimo: Ln(μ, x1, x2, xn)
A Estimatitiva da Maxima Verossimilhanca EMV = n/ Σxi = 1/x = inverso da media amostral
Distribuição Exponencial
Trata-se de um modelo de distribuição para variáveis aleatórias (v.a.) contínuas que seguem um modelo dade pela função densidade de probabilidade:
\[f(x) = \begin{cases} \alpha e^{-ax}, x \geq 0 \\ 0, x < 0 \end{cases} \to -\infty < 0 < \infty\]
\[f(x) = \int_{-\infty}^{x} f(x) \; dx) = \int_{0}^{x} \alpha e^{-dxt} dx \] Onde o parâmetro \(\alpha\) é o intercepto em \(x=0\), ou seja, \(\alpha\) informa o falor onde inicia o decaimento da distribuição e o valor de \(x\) fornece a velocidade do decaimento. Assim,, sew o valor de \(\alpha\) for muito alto ela decai de forma brusca, e o aumento do valor de \(x\) atua acelerando esse decaimento
x <- seq(0, 8, 0.1)
# lambda = 2
plot(x, dexp(x, 2), type = "l",
ylab = "", lwd = 2, col = "red")
# lambda = 1
lines(x, dexp(x, rate = 1), col = "blue", lty = 1, lwd = 2)
# lambda = 0.5
lines(x, dexp(x, rate = 0.5), col = "orange", lty = 1, lwd = 2)
legend("topright", c(expression(paste(, lambda)), "2", "1", ".5"),
lty = c(0, 1, 1, 1), col = c("orange", "red", "blue"), box.lty = 0, lwd = 2)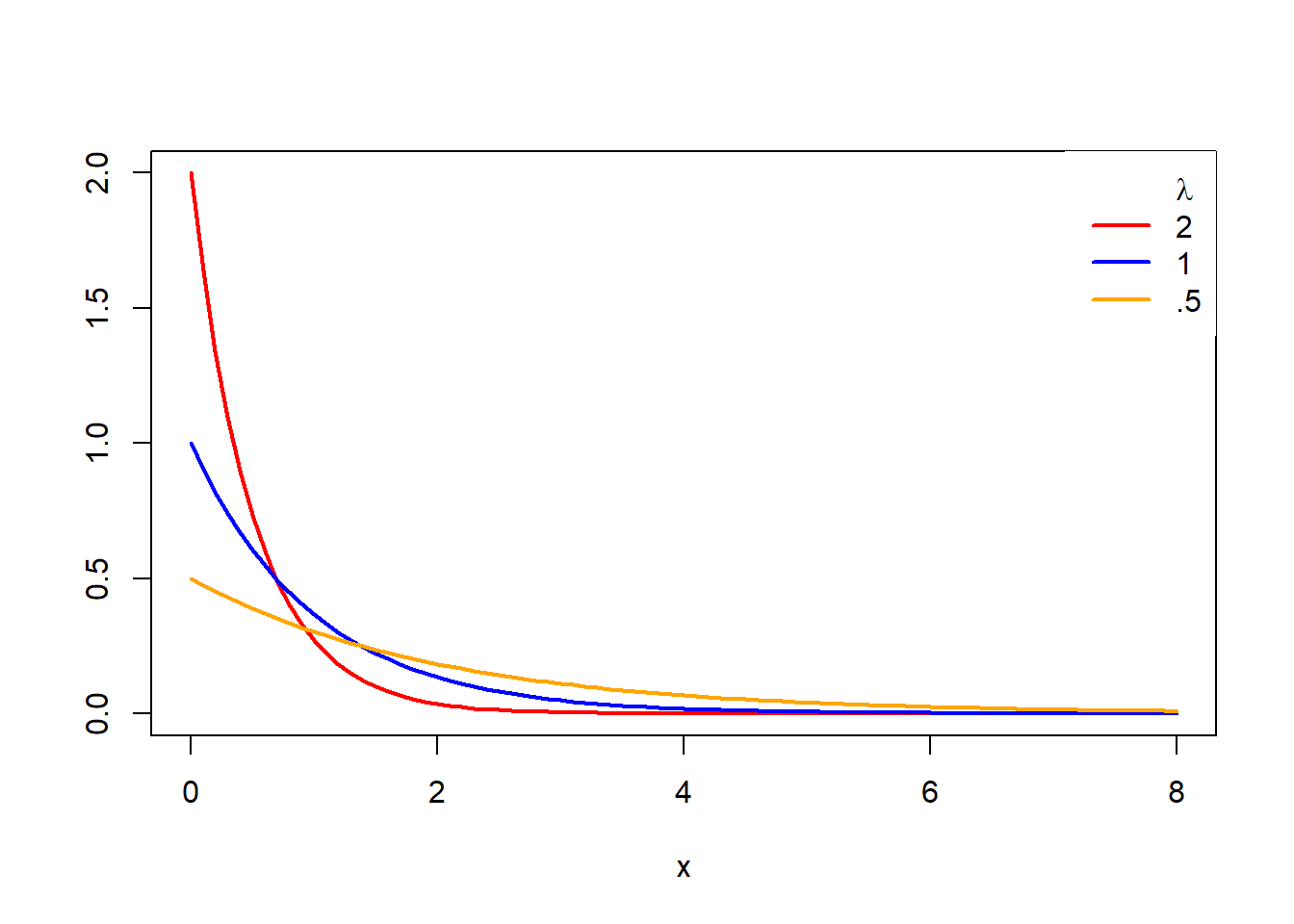
Para a funcão de distribuicão acumulada: \[f(x) = \begin{cases} \alpha -e^{-ax}, x \geq 0 \\ 0, x < 0 \end{cases} \to -\infty < 0 < \infty\]
\[f(x) = p(X \leq x) = \int_{- \infty}^{x} f(x) \; dx) = \int_{0}^{x} \alpha e^{-dx} dx = \alpha \frac{e^{-\alpha x}}{(-\alpha)} \int_{0}^{x} = -[e^{-\alpha x}-1] = 1-e^{-\alpha x}\]
x <- seq(0, 8, 0.1)
# lambda = 2
plot(x, pexp(x, 2), type = "l",
ylab = "F(x)", lwd = 2, col = "red")
# lambda = 1
lines(x, pexp(x, rate = 1), col = "blue", lty = 1, lwd = 2)
legend("topright", c(expression(paste(, lambda)), "1", "2"),
lty = c(0, 1, 1), col = c("red", "blue"), box.lty = 0, lwd = 2)
#lambda = 0.5
lines(x, pexp(x, rate = 0.5), col = "orange", lty = 1, lwd = 2)
legend("topright", c(expression(paste(, lambda)), "2", "1", ".5"),
lty = c(0, 1, 1, 1), col = c("orange", "red", "blue"), box.lty = 0, lwd = 2)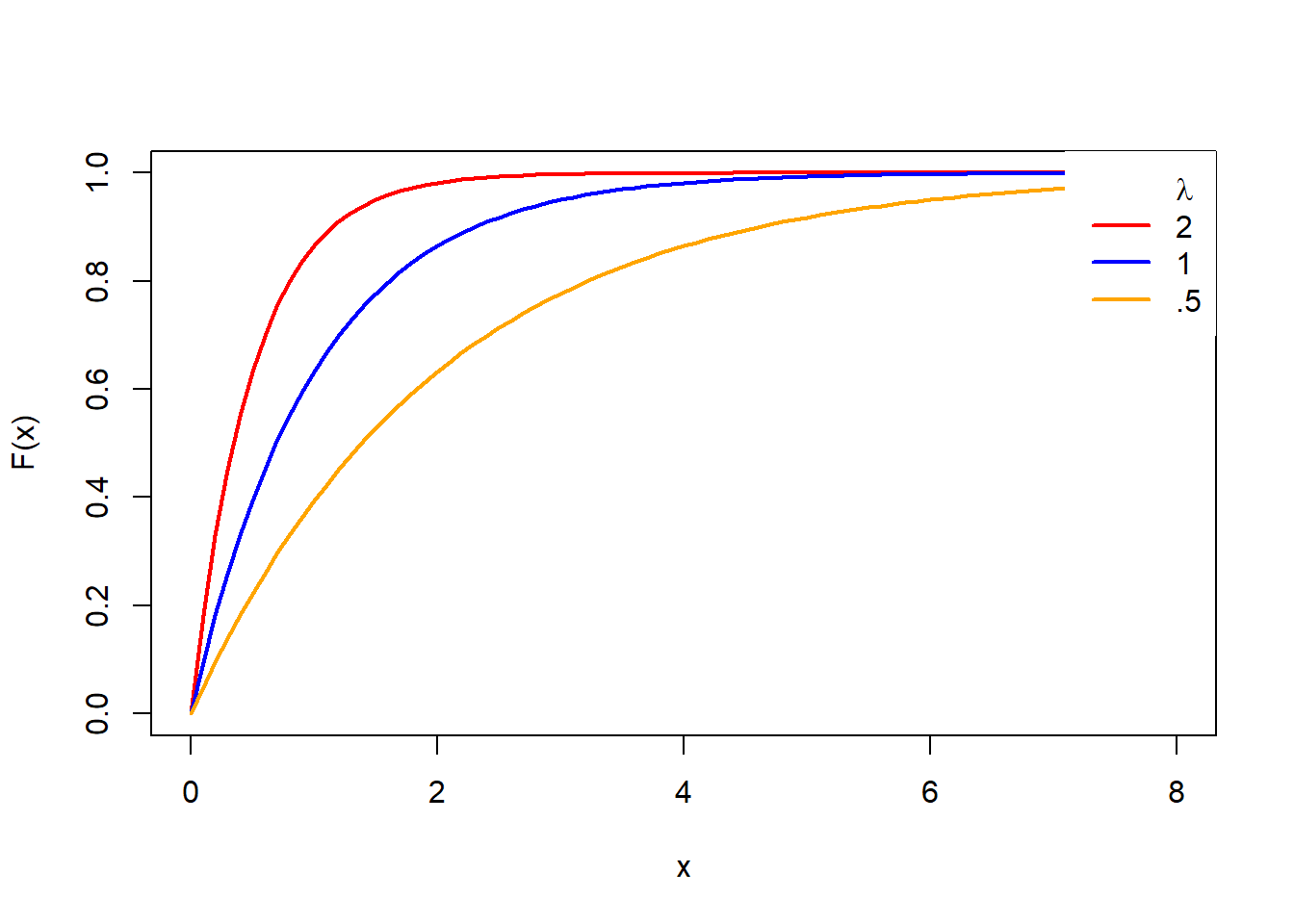
Exemplos
Determinado material radioativo apresenta um intervalo de tempo, em minutos, entre emissões consecutivas dado por uma distribuição exponencial com \(\alpha = 0.2\). Qual a probabilidade de ocorrência de uma emissão em um intervalo menor que dois minutos? \[ T = tempo entre emissões\] \[P(T \leqslant 2) = \int_{-\infty}^{2} f(t) \; dt) = \int_{0}^{2} \alpha e^{-dt} dt = \alpha\int_{0}^{2}e^{-dt} dt = \alpha\frac{e^{-dt}}{(-\alpha)}\int_{0}^{2} = - [e^{-2\alpha}+1] = 1-e^{2*0.2}= 1-e^{0.4} = 0.33 \] \[\therefore 33 \% \]
Distribuicão Expenencial é uma distribuição sem memória:
\[P{x \geq t+s | X \geq s} = P(x \geq t) \] \[ P{x \geq t+s | X \geq s} = \frac{P{x \geq t+s , X \geq s} }{P(x \geq s)} = \frac{p(X \geq t+s)}{P(x \geq s)} = \frac{e^{-\alpha(t+s)}}{e^{-\alpha s}} = \frac{e^{-\alpha t} e^{-\alpha s}}{e^{-\alpha s}} = e^{-\alpha t} \\ \therefore = P(X \geq t)\]
Exemplo
O intervalo de tempo, em minutos, entre emissões consecutivas permanece \(t=0.2\). Agora, qual a probabilidade do intervalo entre emissões ser superior a 7, sabendo que ele é maior do que 5 minutos?
\[ p(T \geq 7 | T \geq 5) = P(T \geq 2) = e^{-2*0.2} = e^{-0.4} = 0.67\] \(\therefore 67 \%\)
Experanca e Variância
\[E[X] = \frac{1}{\alpha}\] \[Var[X] = \frac{1}{\alpha^2}\] \[\therefore E[x] = \int_{-\infty}^{\infty} xf(x) \; dx) = \int_{-\infty}^{\infty} x\alpha e^{-\alpha x}\; dx) = \alpha \int_{-\infty}^{\infty} x e^{-\alpha x}dx\] \[ x = u \\ e^{-\alpha x}dx = vdv\] \[ = \alpha \left[ \frac{x e^{-\alpha x}}{(-\alpha)} - \frac{e^{-\alpha x}}{(-\alpha)} dx \right]_0^\infty = \alpha \left[ 0 + \frac{1}{\alpha}\frac{e^{-\alpha x}}{(-\alpha)} \right]_0^\infty = \alpha\left[-\frac{1}{\alpha^2} [0-1] \right] = \frac{\alpha}{\alpha^2} = \frac{1}{\alpha}\] \[ Var(X) = E[x^2]-E[x]^2 \to \therefore \frac{1}{\alpha^2} \]
Distribuição Binomial
Trata-se de uma distribuição de probabilidade para valores discretos onde o número de sucessos é dado pelo número de eventos esperados dentre um conjunto de n tentativas. nesse modelo cada tentativa possuis apenas dos resultados possíveis, sucesso ou fracasso (binomial) chamada de tentativa de Bernoulli. Além, disso cada tentativa é independente das demais, possuindo portanto probabilidade constante e independente das demais tentativas. Desde já que a variável de interesse ou pretendida nessa distribuição é o número de k sucessos entre as n tentativas descritas como:
\[P(k;n,p) = \binom{n}{k} p^k (1-p)^{n-k}\]
Para k = 0,1,2,….,n onde \(\binom{n}{k}\) é uma combinacão, que fornece a função completa:
\[P(k;n,p) = \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k}\]
Apresentando valor esperado e variância dados por:
\[E[x] = np\] \[var{X} = np(1-p)\]
Exemplos
Quando três dados não viciados são lançados, a probabilidade de que o número 3 seja apresentado mais de uma vez é dada pela soma das probabilidades de k=2 e k = 3, que pode ser dado pela binomial da seguinte maneira: \[f(2;3,\frac{1}{6}) = \binom{3}{2}*\binom{1}{6}^2*(1-\binom{1}{6})^{3-2}\] \[=\frac{3!}{2!*(3-2)!}*\frac{1}{36}*(\frac{5}{6})^1\] \[= \frac{3}{1}*\frac{1}{36}*\frac{5}{6} = \frac{15}{216} = \frac{5}{72}\] e,
\[ \therefore f(3;3,\frac{1}{6}) = \binom{3}{3}*\binom{1}{6}^3*(1-\binom{1}{6})^{3-3}\]
\[=\frac{3!}{3!*(3-3)!}*\frac{1}{216}*(\frac{5}{6})^0\]
\[= \frac{3!}{3!}*\frac{1}{216}*1 = = \frac{6}{6} *\frac{1}{216}*1 = 1 *\frac{1}{216}*1 = \frac{1}{216} \]
e, \[ \therefore \frac{15}{216} + \frac{1}{216} = \frac{16}{216} \] Sendo por fim igual a 7.4074074 %.
Distribuição de Poisson
Tratase de um modelo de distribuição discreta, onde é mensurada a probebilidade de um certo evento independente ocorrer um certo número de vezes em um intervalo de tempo, área, etc. Esta distribuição foi descoberta por Siméon Denis Poisson quando realizava estudos sobre a probabilidade de julgamentos sobre matérias criminais e civis. A distribuicão de Poisson possui apenas um parâmetro chamado lambda (\(\lambda\)) representando o número esperados de ocorrências no intervalo de mensuracão. A funcão de distribuição é dada por:
\[ f(k;\lambda) = \frac{e^\lambda\lambda^k}{k!},\]
e apresentada pela notação \(X ~ Poisson(\lambda)\)
A Esperança de \(X\) e sua variancia são o próprio \(\lambda\):
\[E[X]= \sum_{n=0}^{\infty} \frac{e^{-\lambda}\lambda^k}{k!} = \sum_{n=0}^{\infty} \lambda \frac{e^{-\lambda}\lambda^{k-1}}{(k!-1)!} = \lambda e^{-\lambda} \sum_{n=0}^{\infty}[\frac{\lambda^{k-1}}{(k-1)!}] = \lambda e^{-\lambda} \sum_{n=0}^{\infty}[\frac{\lambda^k}{k!}] = \lambda e^{-\lambda} e^{\lambda} = \lambda\]
e,
\[Var(X)= E(X^2) - (E(X))^2 = \lambda(\lambda+1)-\lambda^2=\lambda\]
Exemplos:
Considere que em uma seguradora a taxa de sinistros é de 0.2 sinistros por dia. Qual a probabilidade de a seguradora no próximo dia atender dois ou mais sinistros, um sinistro ou nenhum sinistro? Para a presente distribuicão, temos uma distribuição de Poisson com \(X ~Poisson(\lambda)\) com \(\lambda=0.2\), logo:
\[P(X = 2) = \frac{e^{-0,2}(0,2)^2}{2!} = 0,0164\]
\[P(X = 1) = \frac{e^{-0,2}(0,2)^1}{1!} = 0,1637\] \[P(X = 0) = \frac{e^{-0,2}(0,2)^0}{0!} = 0,8187\]
Aproximação de Binomial e Poisson
Em situacões que se apresentam com um elevado número de ensaios (\(x\to \infty\))e uma probabilidade extremamente baixa (\(p\to 0\)), o cálculo da binomial se torna dispendioso ao tornar dificil o cálculo da probabilidade de k sucessos.
\[p(k) = P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}\] a mesma expressão pode ser reescrita como:
\[P(X=k)=\frac{n!}{k!(n-k)!}pk\frac{n^k}{n^k}(1-\frac{np}{n})^{n-k} = \frac{n!}{k!(n-k)!}\frac{(np)^k}{n^k}(1-\frac{np}{n})^{n-k}\] ao substituir \(\lambda\) por \(np\):
\[P(X=k) = \frac{n(n-1)...n(n-k+1)}{k!}\frac{\lambda^k}{n^k}(1-\frac{\lambda}{n})^{n-k} = \frac{\lambda^k}{n^k}(1-\frac{\lambda}{n})...(1-\frac{k-1}{n})(1-\frac{\lambda}{n})^{n-k}\]
Assim, se o limite tende ao infinifo (\(n\to \infty\)) se chega em:
\[\lim_{x \to \infty} 1 \biggl(1-{\frac{1}{n}}\biggr)...\biggl(1-{\frac{k-1}{n}}\biggr) = 1\] \[\lim_{x \to \infty} \biggl(1-{\frac{\lambda}{n}}\biggr)^{n-k} = \lim_{x \to \infty} \biggl(1-{\frac{\lambda}{n}}\biggr)^{n} = e^{-\lambda} \] \[\therefore \lim_{x \to \infty} P(X=k)= \frac{e^{-\lambda}\lambda^k}{k!}\]
Exemplos
Em uma fábrica de televisores o controle de qualidade identifica que 0.001% dos equipamentos apresentam falha ao ligar, qual a probabilidade de que em um lote de 4000 televisores, 2 ou mais apresentem a referida falha?
Poisson
Temos: \(\lambda = n.p = 4000*0.00001 = 0.04\)
\[\therefore P(X=2) = 1-P{X=0}-P(X=1) = 1-\frac{0.04^0e^{-0.04}}{0!}-\frac{0.04^1e^{-0.04}}{1!} \approx 1- 0.999221 \approx 0 .00078\]
Distribuição Gama
curve(expr = dgamma(x = x, shape = 2, rate = 2), xlab = "", ylab = "", main = "Gamma Beta = 2", lwd = 2, col = 1, xlim = c(0, 2),
ylim = c(0, 8))
for (i in 1:5) {
curve(expr = dgamma(x = x, shape = 2, rate = c(3, 5, 10, 15, 20)[i]), lwd = 2, col = (2:6)[i], add = TRUE)
}
legend(x = "topright", legend = c("Escala = 2", "Escala = 3",
"Escala = 5", "Escala = 10",
"Escala = 15", "Escala = 20"), lwd = 2, col = 1:6)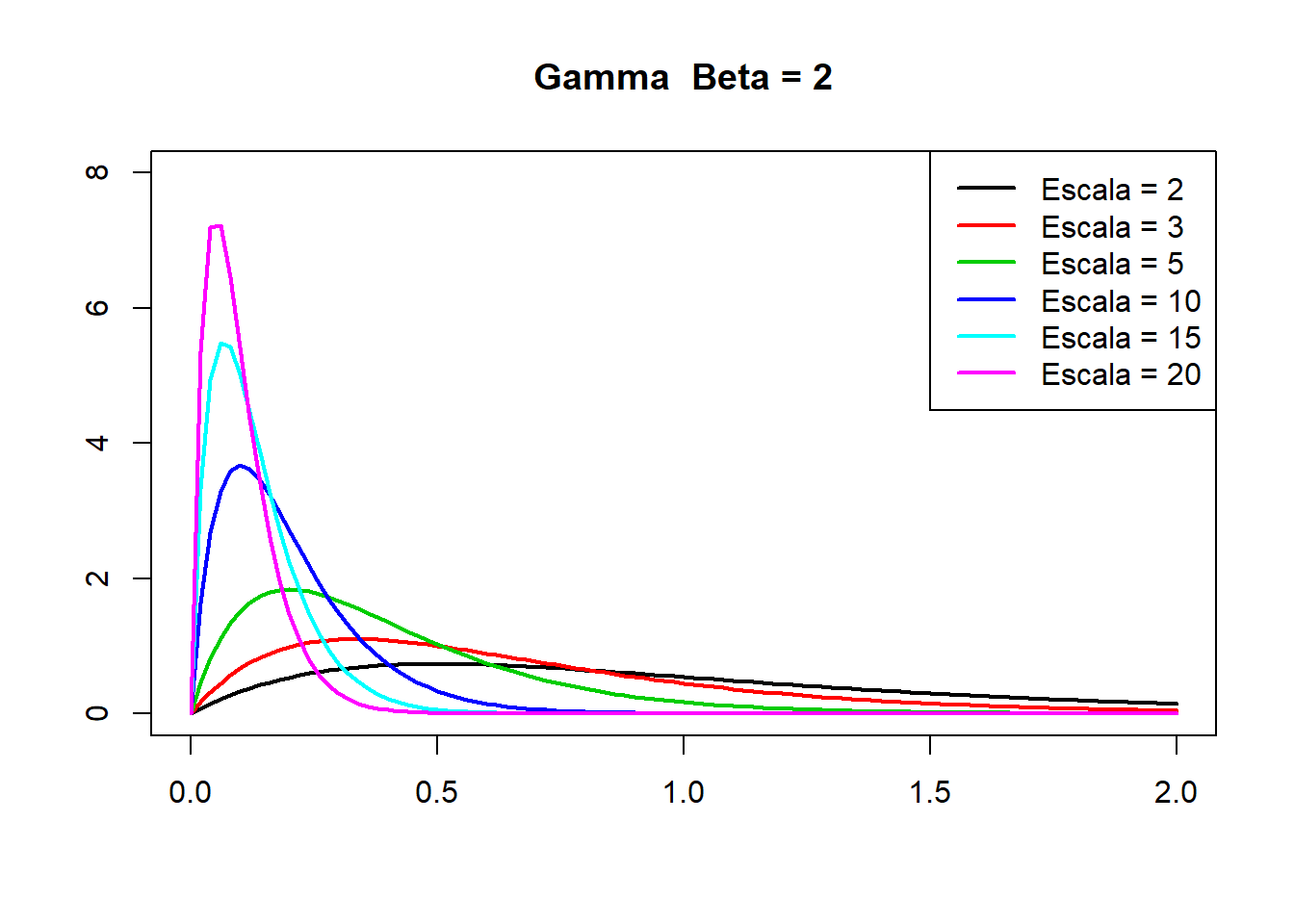
curve(expr = dgamma(x = x, shape = 2, rate = 2), xlab = "", ylab = "", main = "Gamma Lambda = 2", lwd = 2, col = 1, xlim = c(0, 20),
ylim = c(0, 0.8))
for (i in 1:5) {
curve(expr = dgamma(x = x, shape = c(3, 5, 10, 15, 20)[i], rate = 2), lwd = 2, col = (2:6)[i], add = TRUE)
}
legend(x = "topright", legend = c("Forma = 2", "Forma = 3",
"Forma = 5", "Forma = 10",
"Forma = 15", "Forma = 20"), lwd = 2, col = 1:6)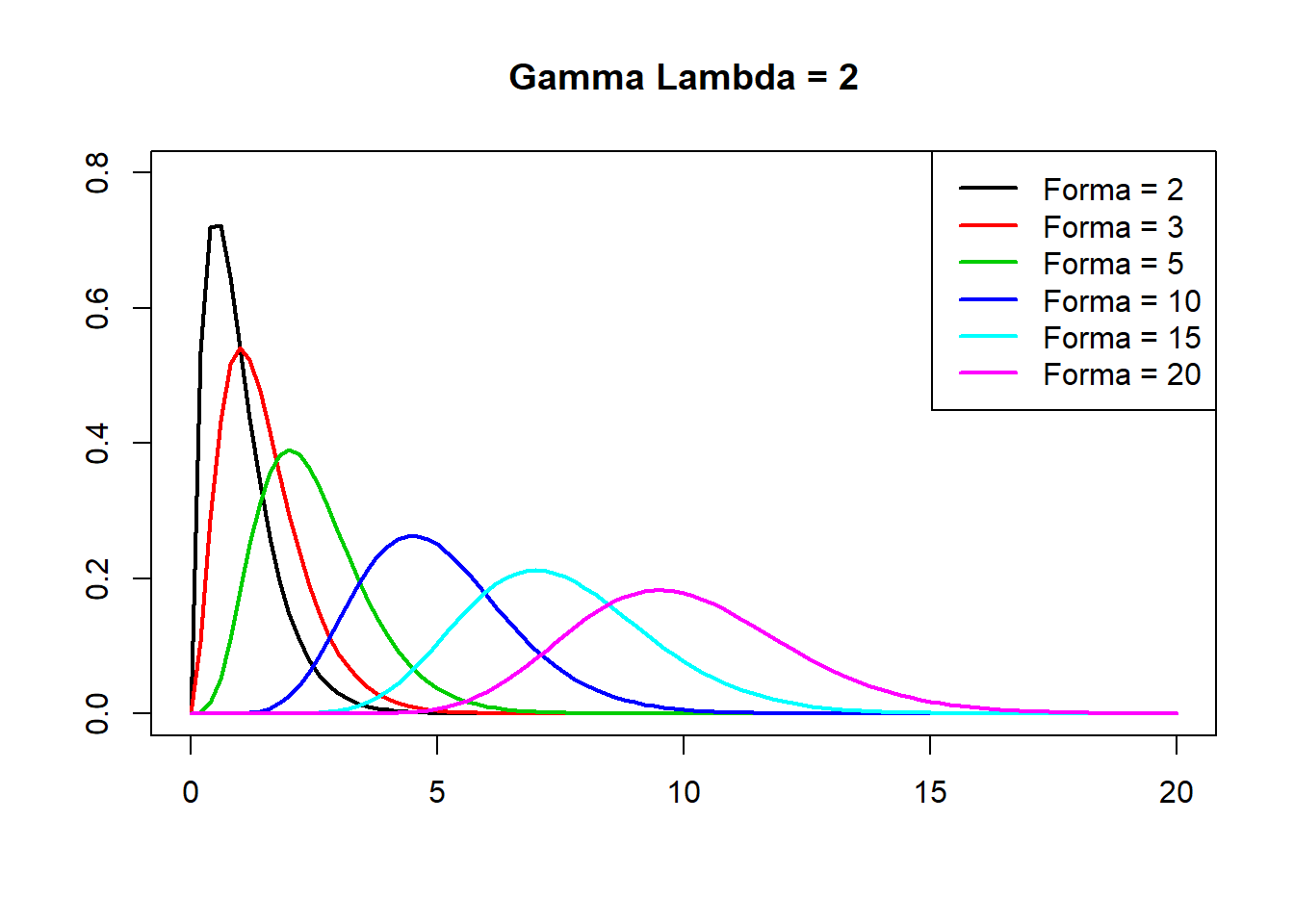
A distribuição gama é uma distribuição de v.a. contínua que descreve o tempo necessário para se obter um número de occorencias de um evento, dado por:
\[f(x) = \begin{cases} \frac{\beta^\alpha (x)^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)} \end{cases}\]
Onde \(\alpha\) é o parâmetro que fornece a forma da distribuicão e \(\beta\) a escala, sendo ambos positivos e \(\Gamma(\alpha)\) é a função Gamma de Alpha.
Exemplo
A renda domiciliar de uma certa localidade é de R$ 1000,00 com distribuição Gama e desvio padrão de R$ 200,00. A) Quais os parâmetros \(\alpha\) e \(\beta\) desta densidade? B) Qual a probabilidade da renda no local exceder os R$ 2000,00?
Se X tem distribuição Gama com parâmetros \(\alpha\) e \(\beta\) a média de X é dada por \(\frac{\alpha}{\beta}\) e a variância por \(\frac{\alpha}{\beta^2}\) e portanto,
\[\mu = \frac{\alpha}{\beta}\to 1000 = \alpha = 1000 * \beta \\ \alpha^2 = \frac{a}{\beta^2}\to 200^2 = \frac{1000\beta}{\beta^2}\] \[\beta = \frac{1000}{200^2} = \beta = 0.025\] \[\alpha = 1000 * 0.25 = 25\]
- \(P(X > 2000) = 1 - P(X \leq 2000)\)
\[p=1-\int_{-\infty}^{2000}\frac{\beta^\alpha (x)^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}dx\] \[p=1-\left[ \int_{-\infty}^{0}\frac{\beta^\alpha (x)^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}dx+\int_{0}^{2000}\frac{\beta^\alpha (x)^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}dx \right]\] \[p=1-\left[ 0+\int_{0}^{2000}\frac{0.025^{25} (x)^{25-1}e^{-0.025 x}}{(\alpha-1)!}dx \right]\] \[p=1-\left[\int_{0}^{2000}\frac{0.025^{25} (x)^{25-1}e^{-0.025 x}}{(25-1)!}dx \right]\] \[p=1-\left[\frac{0.025^{25}}{24!} \int_{0}^{2000} (x)^{24}e^{0.025x} dx \right]\] \[p = 1-0.7456 = 25.44\%\]